리만 가설

리만 가설의 증명을 3일에 걸쳐서 끝까지 따라가 봤다. 리만 가설의 증명을 이해하려면 오일러, 가우스, 뫼비우스, 몽골트, 하다마드, 코쉬등 많은 수학자들의 업적을 이해해야 하고 제타 함수 외에도 감마, 뫼비우스 함수, 소수 계량 함수 등 다양한 함수의 성질들을 이해해야 한다. 아마 수학 매니어가 아니라면 끝까지 사냥하기가 쉽지 않다. 리만의 생애와 업적을 간단히 요약해 본다. 논문 내용은 뒤에 실었지만, 아무도 안 볼 것이라는 것은 알고 있다.

 

물리학에 조금이라도 관심이 있다면, 특히 상대성이론에 관심이 있다면 리만(1826-1866)의 이름은 누구나 들어본다. 일반 상대성이론의 장 방정식 (field equation)이 Riemann tensor로 표현되기 때문이다. 특수 상대성이론은 아인슈타인이 거의 순식간에 해치운다. 물론, 그 전에 수많은 거인들이 초석을 다졌다. 힐베르트와 로렌츠는 사실 수학적으로 아인슈타인보다 훨씬 정교하게 상대성 이론에 접근해 있었다.

 

그러나, 일반 상대성이론은 아이디어를 생각하고도 10년의 작업이 필요했다. 리만의 미분 기하학 (differential geometry)라는 수학적 도구와 수학자 친구 그로스만의 도움이 없었다면 일반 상대성 이론은 탄생하지 못했을 것이다. 특수 상대성이론은 중학교 수학이면 이해가 가능하지만, 일반 상대성이론은 미분 기하학을 모르면 이해가 불가능하다. 밴드 경험상, 대부분은 tensor의 이해에서 막혀서 진도를 나가지 못한다.

 

리만은 1826년 하노버의 작은 마을의 루터교 목사의 아들로 태어난다. 베를린대학과 괴팅겐대학에서 교육을 받고 복소함수론 (complex variables)으로 박사학위를 받는다. 리만이 제타함수를 복소수로 쉽게 확장한 데에는 이러한 배경이 있다. 대학 수학을 이해하는 첫 단계는 해석학이라는 과목을 수강하는 것이다. 해석학에서는 연속, 미분가능, 수열의 수렴에 관한 기본적인 개념과 수학적 언어를 배운다. 미적분의 아이디어는 뉴턴과 라이프니츠가 제공했지만 적분에 대한 엄밀한 수학적 정의와 적분 가능성에 대해서 리만이 연구한다. 해석학을 배우면 Riemann과 Lebesgue integral을 배운다.

 

1854년 괴팅겐 대학의 무급강사가 된 그는 관례에 따라 교수진들 앞에서 논문을 발표한다. 제목은 <기하학의 기초를 이루는 가설에 관하여”였고, 그 발표에서 유클리드 공간의 거리 공식을 일반적인 곡면 공간으로 확장하는 내용을 발표한다. 타인에게 별 관심이 없던 가우스(1777-1855)가 살짝 눈길을 준다. 아래가 그 내용이다. 아래에서 g를 metric tensor라고 부른다.

 

소수는 1과 자신을 제외하고는 자신을 나누지 않는 수이다. 아주 오래 전, 기원 수천년 전부터 인간들을 매료시킨 존재가 바로 소수이다. 정수론 전체가 소수에 관한 얘기를 하고 있다고 해도 과언이 아니다. 1859년 리만은 베를린 학술원에 선정되는데, 선정된 이는 반드시 최근 연구업적을 보고하게 되어 있었다. 이에 따라 그는 몇 페이지 되지 않는 짧은 연구보고서를 제출한다. “주어진 수보다 작은 소수의 개수에 관하여”라는 아주 짧은 보고서이다. 리만 가설은 그렇게 탄생한다. 그 짧은 논문을 읽어보고 증명 과정을 쫓아가 보면, 수많은 쓸데없는 말들의 향연보다, 단 몇 개의 수식들이 존재의 본질을 훨씬 깊이 있게 얘기한다는 것을 느낀다.

 

그 짧은 단 한편의 논문, 분량이 짧았기에 내용 전개가 수학적으로 엄밀하지 않았지만, 그 안에는 그 이후 150년동안 인류가 연구할 많은 내용들이 담겨져 있었다. 가설의 내용은 간단하다. 제타함수의 해(root)가 모두 1/2 + jt 라는 실수 1/2인 직선상에 모두 존재한다는 것이다. 그것을 가정하면 소수의 분포는 비록 random하지만, 어떤 수보다 작은 소수의 개수를 정확히 구할 수 있다. 리만 가설은 제안한지 160여년이 지난 지금까지도 해결되지 못하고 새로운 천재의 출현을 기다리고 있다.

 

1857년 괴팅겐 대학의 조교수로 임명된 후, 1859년에 가우스의 후계자로 괴팅겐 대학의 교수직을 승계한 디리클레 (1805-1859, Fourier 변환 존재 조건, Dirichlet condition으로 유명)가 사망한 후, 정교수로 임명되지만 1866년 40살의 젊은 나이에 폐결핵으로 사망한다. 단 10년이라는 짧은 기간 동안 10여편의  논문만 발표했지만(원래 가우스 파들이 발표에 인색하다. 오일러가 860여편의 논문을 발표한 것과는 극히 대조적이다), 정수론과 비유클리드 기하학에 크나큰 발자취를 남긴다. 안타까운 것은 그의 사 후, 가정부가 집을 정리하면서 미완성 논문들을 모두 불태워 버렸다는 사실이다.

 

그럴일은 없지만, 혹시 리만 가설 증명에 관심이 있다면

 

=================================

 

이전에 포스팅한데로, 인간이 현재까지 아는데로는 소수에는 규칙성이 없다. 다만, 우리는 소수의 분포에 대해서, 즉, 소수들의 모임에 대해서는 조금은 얘기할 수 있다. 그 시작은 오일러가 조화급수를 연구하면서 찾아낸 제타함수에서 시작한다. 즉, 제타함수의 값은 소수들의 무한곱과 관련이 있는 것이다. 오일러 곱(Euler product)라고 불린다.

 

그 다음은, 15살 때 가우스가 찾아낸 아래 소수 계량 함수(prime counting function)이 있다. 이것은 어떤 양의 실수 x보다 작은 모든 소수의 개수를 어떻게 구하느냐는 문제이다. 경험 법칙으로 가우스는 아래와 같은 함수를 만든다. 이것을 소수 정리 (prime numbery theorem)라고 부르는데, 르장드르, 가우스 모두 증명에 실패하고 리만의 아이디어를 바탕으로 1896년 Hadamard가 증명한다. 아래에서 li(x)를 logarithmic integral function이라고 부르며 좀 더 정확한 값을 출력한다.

 

1850년 리만은 먼저 제타함수를 실수뿐 아니라, 전체 복소수 영역으로 확장한다. 복소 영역에서 정의된 함수이기 때문에 오일러가 아니라 리만의 제타함수라고 부른다. Complex function (복소 함수)은 해석학에 있어서 아주 중요한 함수이며, 복소 함수를 이용하면 이전에 불가능했던 수많은 적분을 아주 쉽게 계산할 수 있다. Residue theorem이라고 해서, 분모가 0이 되는 값, pole 위치에서의 함수의 값만으로 계산이 가능하기 때문이다.

 

먼저, 아래와 같이 제타함수를 재 정의함으로써 s>0 영역 전체로 확장한다. 이것을 meromorphic function이라고 부른다. 물론, s=1, 즉 분모가 0인 점은 제외이다. 원래의 수열은 s<=1이면 발산하지만, 즉, 0<s<=1에서 정의되지 않지만, 아래 식으로 정의된 제타함수는 s>0에 대해서 정의된다. 아래에서 첫번째 과정이 Abel’s lemma로 불리는 과정이다.

 

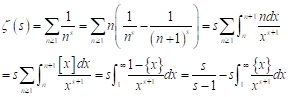
이제 전체 복소 평면으로 함수를 확장하기 위하여 먼저, 아래와 같이 리만 제타 함수를 재 정의한다. 상세한 과정은 이과 출신들도 거의 쫓아가지 못할 것이니, 가볍게 skip 하시면 된다 (물론, 나는 끝까지 사냥했음 ^^). 이 과정에서 오일러가 만든 Gamma함수의 성질도 알아봐야 한다. 이 함수는 n! 함수를 실수 전체에 대해서 확장하기 위하여 Euler가 만든 함수이다. 물리학 전분야에서 특히 양자역학에서 자주 만나게 되는 함수이다.

 

이제 양변에 s(s-1)/2를 곱하여 리만 xi 함수를 아래와 같이 정의한다.

 

리만 제타함수는 s>1영역에서 수렴한다. 따라서 s>1영역에서는 어떤 s에 대해서도 근을 가지지 않는다. 따라서 위에서 정의된 xi함수는 s>1 영역에 zero를 가지지 않는다. Xi(s)=xi(1-s)라는 관계식으로부터 s<0에서도 마찬가지로 zero를 가지지 않는다. 따라서 모든 해는 0<s<1사이에만 가진다. 이 영역을 critical region 혹은 critical band라고 부른다.

 

리만이 몇 개의 해를 구해보니 리만 제타함수의 모든 non-trivial solution은 모두 real part, 실수부가 1/2인 라인선상에 존재하였고, 이것으로부터, 그 유명한 리만 가설, Riemann conjecture를 만든다. 즉, “리만 제타함수의 모든 비자명 해는 1/2+it라는 라인상에 존재한다”가 그것이다. 그리고, 1921년 Hardy와 littlewood는 그 근의 수가 무한개임을 밝혀낸다.

 

Riemann의 소수계량함수 J(x)와 정확한 소수계량함수 사이에는 아래와 같은 관계식이 있으며, 둘 중 하나를 알면 나머지를 아래 식에 따라 구할 수 있다. 아래에서 mu(n)은 뫼비우스 함수라고 불리며, 어떤 수가 짝수개의 서로 다른 소수로 분해되면 1, 홀수개로 분해되면 -1, 다른 모든 경우는 0이다.

 

리만 소수 계량 함수 J(x)와 제타 함수 사이에 위에서 본 것과 같은 라플라스 변환 관계에 있기 때문에, J(x) 는 아래식과 같이 역변환을 할 수 있으며,

 

앞에서 구한 Riemann xi 함수의 root는 원래 zeta 함수의 nontrivial에 해당하며, 이제 아래와 같이 zeta함수를 root로 표시할 수 있다고 가정해 보자. 그러면 아래와 같이 log zeta 함수와 root사이에 아래와 같은 관계식이 존재한다.

 

이제 이 관계식을 J(x)를 구하는 적분식에 넣어서 적분을 계산하면 아래와 같은 관계식을 얻는다. Li(x)는 log integral function이다. Li(x)함수는 x/log(x)보다 정교하게 소수의 개수를 세지만, 정확한 개수보다 좀 더 많이 세게된다. 리만이 위의 많은 작업의 결과로 아래와 같이, 제타함수의 비자명해를 이용하여 거의 정확히 소수의 개수를 세는 방법을 만들어 낸다.

 

리만 소수계량함수로 계산한 값과 실제 값은 아래에서  보듯이 정교하게 일치한다.