우주 방정식, 프리드만 방정식

 

이전 포스팅에서 우주 전체를 기술하는 metric을 얘기하였다. Robertson, Walker가 만들고 Friedman이 활용한 FRW metric이다. 다시 기술하면 아래와 같다.

 

만약, 우주의 한점에서 똑바로 이동을 하면, 간단히 얘기해서 연료를 끄고 관성에 의해서만 geodesic line을 따라 이동하면 원점으로 되돌아 올까? 이전 포스팅의 3차원 구의 표면에 해당하는 2차원 공간을 생각해 보자. 이 경우, geodesic line은 현재 점을 따라 구의 표면을 따라 대원을 그릴 것이고 한 지점에 깃발을 꽂고 계속 이동하면 원래의 점으로 되돌아온다. 즉, 곡률이 양이라면 닫힌 우주 (closed), 이 경우 원래 출발한 점을 주기적으로 지나게 된다. (물론, 우주가 팽창하기에 그렇지는 않다.) 이것을 수식으로 확인해 보자. 내가 현재 서 있는 곳이 원점이고, 즉 (t,r,theta, phi)=(0,0,0,0), 현재의 시간에 거리 r만큼 떨어진 지점의 좌표는 (0,r,0,0)하고 하면 두 지점 사이의 proper distance l은 아래와 같이 구할 수 있다.

 

만약 k=0이라면 r=l/a가 되어 l이 증가하면 r도 계속 증가한다. 즉, 영원히 바깥으로 진행한다.경계가 없다.

만약 k=1이라면 아래 식과 같이 l이 증가하면 주기적으로 원래점으로 돌아온다. 닫힌 우주이다.

 

만약 k=-1이라면 아래 식과 같이 l이 증가하면 주기적으로 원래점으로 돌아온다. 무한대의 열린우주이다.

 

================

프리드만 방정식은 우주 전체의 운동을 기술하는 방정식이다. 여기서 은하수는 그냥 한 점에 불과하다. 아인슈타인의 장방정식을 FRW metric에 적용하면 나오는 방정식이다. 이 방정식은 두개로 구성되는데, 먼저 첫번째 방정식은 아래와 같다. rho는 물질들의 밀도, k는 곡률, lambda는 우주 상수이다.

 

그리고 두번째 방정식은 아래와 같다.

 

프리드만 방정식은 고전적인 뉴턴 방정식으로 부터도 유도가 가능하고, FRW에 Einstein 의 field equation을 적용해도 유도가 가능하다. 후자의 경우는 계산이 상당히 복잡하다. 먼저, 고전적인 역학 방정식에서 유도를 해 보자. 아래와 같이 나의 위치에서 반경이 r인 원을 그려보자.

 

1.mass conservation: 먼저 반경 r안의 물질들의 질량이 변하지 않는다고 가정하면, 아래와 같이 질량 밀도와 확장 계수 사이의 관계식을 얻을 수 있다.

 

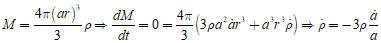
2.Accleration: 간단한 뉴턴 역학 방정식 F=ma를 적용하면 아래와 같이 첫번째 Friedmann 방정식을 얻는다. 단, 아래의 수식은 radiation이 없는 경우, dust 만 존재하는 경우, p=0인 경우에만 적용이 가능하므로, 완전한 Friedmann 방정식은 아니다. 또한, 우주 상수 부분도 고려할 수 없다.

 

앞의 가속도 방정식의 양변에 R’(t)를 양변에 곱해서 정리하면 아래와 같이 두번째 Friedmann 방정식을 얻는다.

 

다음 포스팅에서는 Einstein 장방정식, 일반상대성이론을 적용하여 Friedmann 방정식을 구하는 과정을 적을 예정이다. 그것은 위의 과정보다 훨씬 지저분한 계산을 해야 하기에 방법론만 설명한다.