천문학과 열역학

 

이 시대에 baryon과 photon의 밀도는 대략 10^9정도로 photon이 많다. 그러나 baryon (예를 들면 양성자 한 개)의 에너지는 931MeV~10^9eV정도이고, 우주에서 가장 많은 CMB photon은 2.7K~2.3x10^-4eV 정도로 그 둘의 에너지 비는 10^13정도로 baryon의 에너지가 많다. 복사, radiation은 더 이상 우주 팽창에 기여를 하지 못한다. 그러나 이러한 복사와 물질의 역전은10^10s, 우주의 온도가 10eV정도로 떨어진 시간부터 시작한다. 우주의 초기에는 복사(photon)가 팽창을 주도한다.

삭제

 

Metric, 자의 눈금이 계속 커지고 있다. 만약 과거에도 이러한 팽창의 법칙(Hubble's law)이 유효했다면, 현재 우리 눈에 보이는 우주는 138억년전에는 한점에서 시작했을 것으로 추정된다. 물질/에너지가 보존된다고 가정하면, 우주의 초기에 온도는 상상을 초월할 정도로 높았을 것이다. 이것이 빅뱅의 얘기이다. Big bang이라는 용어 때문에, 인간들은 무엇인가가 터졌다고 상상한다. 그렇지는 않다. 현재의 observable universe가 오랜 과거에는 한점에서 출발했을 것이라는 우주 초기 조건에 대한 기술에 불과하다. Big bang은 이러한 어처구니 없어 보이는, 전 우주가 원래 한점이었다는 신화적인 얘기를 조롱하기 위해 나온 용어이다.

 

지난 몇번의 포스팅으로 우주 단위의 metric, 우주 단위의 동역학, 우주의 팽창 속도와 에너지 밀도의 변화를 얘기하였다. 이번에는 우주의 역사를 통한 우주의 온도 변화를 얘기할 것이다. 온도 혹은 에너지 레벨이 달라지면 물리 현상은 지금과 다르다. 우주의 초기에 존재한 많은 입자들은 사라지고, 현재에는 바리온과 렙톤, 메종 입자들이 존재한다. 현재의 물리법칙, 강력/약력/중력/전자기력은 원래부터 존재한 것이 아니라, 에너지 레벨이 일정 수준이하로 떨어지면 나타나기 시작한다.

 

온도를 얘기하려면 열역학을 얘기해야 한다. 물리학을 이해하려면 먼저 기초적인 수학 지식이 필요하다. 몇 개만 나열해보면, (미적분학(calculus), 선형대수(linear algebra), 미분방정식(differential equation), 미분기하학(differential geometry), 현대대수학(abstract algebra), 확률변수(random variable))들이다. 그 다음에는 고전역학, 전자기학, 열및통계역학, 양자역학, 특수/일반상대성이론, 양자장론, 입자물리학 순으로 물리학 주요 과목을 이해하면 된다.

 

1.Bose Einstein, Fermi-Dirac statistics

 

통계 역학의 결과에 따르면 energy state E를 어떤 전자가 점유할 확률은 fermion의 경우 Fermi-Dirac statistics를 따르고, boson의 경우, Bose-Einstein statistics를 따른다고 알려져 있다. 그 두 통계는 아래와 같은 단일 식으로 표현이 가능하며, 결론적으로, 어떤 에너지 레벨 E에 존재하는 전자밀도, number density는 아래와 같이 주어진다. 아래에서 g는 degree of freedom을 나타낸다. 보통은 g=2이다. Photon의 경우 helicity 자유도, Fermion의 경우 스핀 자유도이다 (up/down). 그리고 mu 는 chemical potential 이라고 부르는 양이며 mu=-TdS/dN 정의되며, 반응의 전후로 입자들의 분포의 변화를 의미한다.

 

 

열역학 기본 방정식을 다시 한번 remind 해 보자. 아래에 열역학에서 말하는 여러 용어들이 나온다. U는 내부에너지이고, A는 헬름홀츠 자유에너지, H는 엔탈피, G는 Gibbs 자유에너지이다.

 

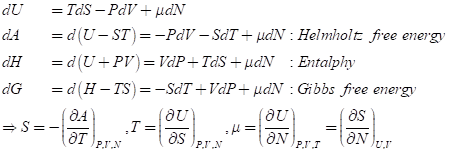
2.state density

Time independent Schrodinger 방정식과 그 해로부터, state, number, energy density를 다음과 같이 구할 수 있다. 수식이 복잡해 보이지만, 어려운 것은 아니다.

 

위에서 값을 구하려면 적분값을 계산해야 하는데, closed form으로 나오는 것은 아니다. 그러나 만약 m<<1, 즉, 우주의 온도가 높아서 입자들이 상대론적인 속도로 움직인다면, 그래서 대부분의 에너지가 운동에서 기인한다고 가정하면 아래와 같은 방정식을 적용할 수 있다. 참고로 Rieman zeta function과 Gamma function에 대해서도 아래 수식에서 기술하였다.

 

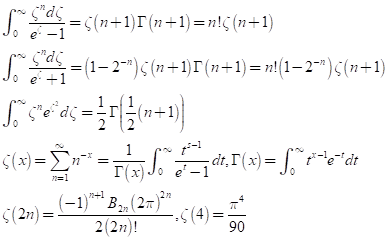
위의 함수들을 이용하여 입자와 에너지 밀도함수를 구해보면 다음과 같다. (c=h_bar=k=1이라고 가정)

 

위의 공식을 CMB photon에 적용해 보면, T=2.73K이므로 아래와 같다. 지금도 주변에 돌아다니는 수많은 photon들, 137억년전 photon들이 내 뺨을 쉴세 없이 어루만지고 있다. 세상의 광자중 가장 많은 광자가 CMB 광자, 태고적 광자이다. 수많은 별들이 쏟아내는 photon은 밤하늘 전체를 비추는 빛의 10%에 불과하다. 단지, 너무 차갑고 온도가 낮기 때문에 밝게 느끼지 못할 뿐이다.

 

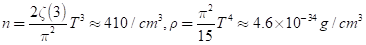
다양한 입자들이 기여하는 것을 고려하면 온도와 에너지밀도 사이의 관계식은 아래와 같이 주어진다. 아래 수식에서 b는 boson을, f는 fermion을 나타내는 첨자이다. 입자들의 내부 자유도 g에 대해서 다음에 상세히 기술한다.