인류 3대 수학자 중 한명, 가우스

수학에 아무리 관심이 없더라도 가우스(1777-1855)의 이름은 피해 나갈 수 없다. 일단 중학교에서 어떤 수를 넘지 않는 최대 정수로 정의되는 가우스 기호 혹은 함수를 배운다. 고등학교에 들어가면 확률론에서 정규 분포(가우스 분포)를 배운다. 또한, 등차 수열의 합 1+2+3+…n=n(n+1)/2 공식을 가우스가 10살에 만들었다는 전설도 누구나 듣는다.

 

가우스는 독일 브라운슈바이크의 벽돌굽는 일을 하는 가난한 가정에서 태어난다. 아버지는 그가 자신과 같이 노동자가 되길 원했으나 어머니와 삼촌의 지원으로 학업에 정진한다. 브라운슈바이크 공작의 지원으로 브라운 슈바이크 공대 업옵후 괴팅겐 대학교에서 근무한다. 그는 흔히 아르키메데스, 뉴턴과 함께 3대 수학자로 회자된다 (오일러가 빠진 것이 사실 의외이다). 이것은 역시 위대한 수학자인, 클라인 병으로 유명한 클라인(1849-1925)이 “그에 비견할만한 역사상 위인은 아르키메데스와 뉴턴뿐이다”라고 말한데 기인할 지도 모른다.

 

작도는 자와 컴퍼스만으로 도형을 그리는 것이다. 이전 포스팅에서 작도가 사칙연산과 root로 이루어진 대수체계임은 설명하였다. 정다각형을 작도로 그릴 수 있는가? 이것은 유클리드의 기하학원론에서 많이 취급하는 문제였고, 정 3/4/5각형과 각의 이등분 작도는 유클리드가 정리해 두었다. 이를 토대로 유클리드는 정 3x2^n, 정 4x2^n, 5x2^n은 작도 가능함을 알아낸다. 즉, 3,4,5,6,8,10,12,16,20,… 각형의 작도가 가능하다. 그리고 꾸역꾸역 정 15각형의 작도법도 오래전에 찾아낸다.

 

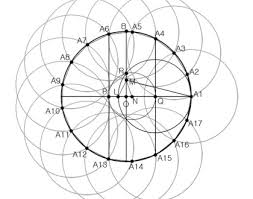
이게 마지막인가? 정 (7,9,11,13,17,19…)각형은 작도가 불가능한가? 인류가 2000년동안 고민했지만 더 이상 한 개도 발견 못한 것을 가우스는 단숨에 정 17각형이 적도 가능함을 증명하고, 그 외 적도 가능한 도형의 공식을 만든다. 1796년의 일이니, 가우스가 19살때의 일이다. 이를 가장 자랑스럽게 여겨서 자신의 묘비명에 정 17각형을 새겨달라고 했지만 그의 묘비에는 “짧게 그러나 완벽하게”라는 문구만 새겨져 있고, 고향 브라운슈바크의 기념비에 대신 정17각형을 새겼다.

 

그리고 가수스는 대수학 기본정리를 증명한다. 대수학 기본 정리는 (fundamental theorem of algebra) 실수 계수를 갖는 모든 다항식은 최소한 1개 이상의 복소수 해를 가진다는 것이다. 다른 말로는 모든 다항식은 실수 계수의 1차 혹은 2차 방정식의 곱으로 나타낼 수 있다는 것이다. 1799년(22살)학위 논문으로 발표하고 1849년(82살)에 실수 계수에 대해서 엄밀히 증명한다. 복소 계수에 대한 증명은1806년 아르강이 최초로 제시한다.

 

너무나 당연해 보인다. 기본정리는 프랑스 수학자 달랑베르(d’Alembert, 1717-1783)에 의해서 제기되었고 누구나 이것이 맞을 거라고 생각했지만 17세기까지 아무도 증명을 하지 못한 것을 가우스가 최초로 증명한다. 오일러, 달랑베르, 라그랑주 같은 대가들이 모두 엄밀한 증명에 실패한 것을 가우스가 최초로 증명한 것이다.

 

가우스는 나이 30에 괴팅겐 대학의 천문대장이 되어 평생 이 직업에 종사한다. 비텐베르크 수학교수 티티우스와 베를린 천문대장 보데가 각각 1766/1772년에 독립적으로 티티우스-보데의 법칙을 발견한다. 지구와 태양사이의 거리를 1AU(1억5천만 km)로 하면 n번째 행성의 평균거리 a=0.4+0.3x2^n 이라는 것이고, 정수 n 마다 행성이 위치한다는 경험법칙이다. 1781년 허셀이 자신의 망원경으로 천왕성을 발견한다. 그것조차도 보데의 법칙을 따르자, n=3의 위치에서 발견되지 않은 행성을 찾아 나서고 1801년 팔레르모 천문대장 피아치가 세레스(Ceres)을 발견하지만 곧 놓쳐버린다. 가우스는 정확한 계산으로 그 궤도를 찾고 그에 따라 천문학자들은 다시 세레스를 찾아낸다.

 

또한 물리학 분야에서 베버(Weber)와 공동 연구하여 전자기학에도 많은 공헌을 한다. 오늘날 자기력의 기본 단위가 가우스(Gauss)이다. 또한 지구의 자기장을 정밀하게 측정한다. 그 외 광학, 모세관 현상, 해밀턴 원리 등 많은 분야에 그의 이름을 남긴다.

 

가우스는 논문 발표를 꺼렸는데, 이것은 뉴턴의 경우와 유사하다. 오일러가 886편의 논문을 쏟아낸 반면 가우스의 발표 논문은 손을 꼽을 정도이다. 완벽주의적인 그의 성격 때문일 것이다. 또한 자신보다 수준이 낮은 학자들이 그의 논문을 평가하는 것에 대한 거부감도 컸다. 그러한 성격 때문에 제자들 양성에도 사실 소홀하였고 이는 후대에 비판의 대상이 된다 (뉴턴도 마찬가지로 혼자 일을 하는 것을 좋아했다). 그러나 그의 제자중 데데킨트, 리만, 베셀등이 있으니 꼭 그렇다고 할 수도 없다.

 

만약 그가 제자를 양성하고 미발표 논문들을 모두 발표하였다면 아마 수학 역사가 최소한 50년은 앞당겨졌을 것이라고 수학사가인 에릭 템플 벨이 얘기한다. 사실, 훗날 발표된 중요한 수학적 내용들이 가우스의 노트에 메모처럼 남겨진 사례는 차고 넘친다. 그 중 하나가 해밀턴이 15년에 걸쳐 발견한 기묘한 수인 4원수의 발견이다. 가우스의 노트에 아주 간략히 적혀있다. 또한 비유클리드 기하학을 30대에 이미 연구했다고 그의 친구에게 말하여 의절한다.

 

"어떠한 사람이라도 나처럼 깊이, 또 부단히 수학적 진리에 몰두하면 그들도 마찬가지의 일을 할 수 있다." 이것은 그가 가장 존경한 뉴턴이 말한 "언제나 그 일을 계속 생각함으로써 발견할 수 있다."는 말과 유사하다.