P, NP 문제

 

#물리학 #양자역학 #양자정보이론

 

슈뢰딩거의 고양이를 모르는 이들은 거의 없을 것이다. 양자역학적으로 동작하는 센서에 독극물 스위치를 연결하고 box를 관측하지 않은 상태로 고양이를 둔다. 그러면, 이론적으로는 고양이는 살아있는 상태와 죽은 상태의 중첩 즉, |cat alive> + |cat dead> 의 양자상태에 놓이게 된다. 살아있는데, 동시에 죽었다... 이것을 어떻게 해석해야 할 것인가? 현대적인 양자역학적 해석은 무엇일까는 양자역학의 본질, 관측이란 무엇인가에대한 화두로 연결된다.

 

슈뢰딩거의 고양이를 현실에서 구현하고자 물리학자들이 열심히 노력하고 있다. 2011년에 430개의 원자로 구성된 Fullerene C60 분자로도 양자역학적인 성질을 관측했다는 논문이 nature 지에 실렸다. ("Quantum interference of large organic molecules") 이렇게 큰 분자를 이중 슬릿을 통해서 통과시켜도 간섭 무늬 패턴이 발생한다는 것을 보인 것이다.

 

그러나 이러한 실험은 실용적인 목적에서는 큰 의미가 없다. 만약에 컴퓨터를 양자역학적으로 구성한다면? 얘기는 완전히 달라진다. 그리고, 그러한 시도는 80년대 들어서 조금씩 이루어지다가 최근 몇년간 많은 대기업에서 많은 연구비를 투여하여 적극적으로 연구중이다. 2019년말, 구글이 53 Qbit으로 구성된 양자 컴으로 기존 컴퓨터가 수만년이 걸려야 풀 수 있는 문제를 풀었다고 발표하여 "양자 우월성" 논쟁을 촉발하였다. 구글과 IBM은 이 분야의 대표적인 선두기업인데, IBM은 바로, 그 문제는 고전 컴퓨터로도 몇개월이면 풀수 있는 문제라고 반박하였다. 

 

 

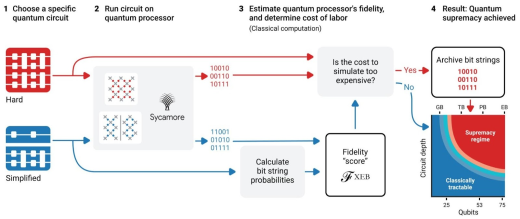
양자 컴퓨터는 양자역학에서 상태들이 중복해서 존재할 수 있다는, superposition principle을 이용하여 어떤 문제를 quantum parallelism을 이용하여 빠른 시간에 풀 수 있는 컴퓨터를 말한다. 예를 들면, |0>과 |1>의 상태도 가능하지만, 양자역학적으로는 x=|0>+|1>의 중첩된 상태, 즉 슈뢰딩거의 고양이가 존재할 수 있기 때문에, 그 중첩된 상태를  f(x)에 대입하면 f(0)와 f(1)을 동시에 계산할 수 있다는 점을 이용한다.

 

어떤 문제가 풀기 쉽다 혹은 어렵다고 우리들은 흔히 말한다. 그러나, 정확히 어떤 의미로 이 문제가 어렵다고 얘기하는 것인지 얘기하라고 하면, 쉽게 대답을 못한다. 컴퓨터공학 분야에서는 어떤 문제가 풀기 어렵다고 얘기하면 보통은 그 문제의 parameter의 개수가 N개일때, 그 문제를 풀기 위해서 지수함수적으로 즉, 2^N으로 증가할 때 어렵다(hard)고 얘기하고, 다항식적으로, 예를 들면 (N^3)으로 계산량이 증가할 때 쉽다(easy)고 얘기한다. 양자컴퓨터는 어려운 문제를 풀기 위해서 개발중인 컴퓨터이다.

 

이와 관련 예전에 써 둔 글을 다시 게시해 본다. 별로 재미있거나 쉬운 내용은 아니니, 관심있는 분들만 읽어보시면 될 것이다.

 

=================================

 

한 문제만 풀어도 100만 $를 받을 수 있는 clay 수학 문제중 유일하게 푸앙카레 가설만을 페렐만이 풀었다. 잘 알다시피, 그는 수상도, 상금도 거부하고, 지금도  상트페테르부르크에서 어머니를 모시고 독신으로 은둔 중인 듯 하다. 

 

나머지 문제들 중 하나의 문제가 P-NP 문제란 것이다. 어떤 문제의 해법을 다항 시간에 풀 수 있으면, 예를 들어 n개의 숫자를 크기 순으로 정렬한다면 프로그램을 잘 못해도 O(n^2)의 시간이면 짤 수 있다. n^2은 다항식에 해당하므로 이러한 문제를 P 문제라고 한다. 반대로 그 문제를 풀기 위해서 exponential 시간, 즉, 2^n의 복잡도를 요구하는 경우, 이것은 NP (non-polynomial) 문제라고 하느냐? 하면 그것은 아니고 NP 문제란, 답이 주어진 경우에 그것을 다항 시간안에 확인 할 수 있는 문제를 말한다.

 

해밀턴 경로 문제가 있다. 지도에 여러 도시가 있는데, 모든 도시를 한번만 방문하는 경로가 존재하느냐를 묻는다. 만약 어떤 사람이 주먹구구로 답을 찾아서 보여주면 우리는 그것이 답인지는 다항시간안에 알 수 있다. 그러나, 그러한 경로를 쉽게 찾을 수 있는 알고리즘은 없다 (n! 소요 -> non-polynomial). 그러한 문제를 NP 문제라고 한다.

 

P-NP 문제란, P=NP이냐 아니면 P=~NP이냐이다. 즉, 모든 NP 문제는, 답을 쉽게 확인 할 수 있는 문제는, P 문제이냐 (즉, 쉽게 문제를 해결할 수 있느냐)? 아니냐를 수학적으로 검증하면 된다. 이것을 증명하려는 많은 시도가 있었고 지금도 있지만, 현재까지는 모두 실패... 일견의 감은 P는 NP와 같을리가 없을 듯 하다. 우리가 답을 쉽게 확인한다고 답을 쉽게 찾을 수 있다는 논리는 이상하기 때문이다. 

 

P-NP 문제를 해결하면 밴친 분들은 수학계의 영웅이 되고, 100만달러를 받게 되고 40이하이면 필즈 메달, 아니면 노벨상에 근접할 수도 있다. 그만큼 이 문제 해결이 미치는 파급 효과가 크다. 당장 우리가 사용하는 보안 시스템의 경우 P=~NP라는 가정하에 시스템이 설계되어 있다. 즉, 어떤 수가 주어졌을 때 이것을 소인수 분해하는 빠른 알고리즘은 존재하지 않을 거라는 믿음이 있다. 그런데 만약 P=NP라면, 이 믿음은 깨어지게 되고, 현재의 보안 시스템의 설계를 다시해야 한다.

 

조금 더 사족을 달아보자. 어떤 문제 A가 주어졌다고 하자. 만약 모든 NP 문제를 A를 사용해서 풀수 있다면 (즉, A문제로 치환할수 있다면) 이것을 NP-hard 문제라고 부른다. 만약 A가 NP 문제라면 이것을 NP-complete 문제라고 부른다. 만약 NP-complete 문제를 한문제라도 쉽게 푸는 (다항시간안에 푸는) 알고리즘을 만든다면 NP->NP-complete->P 룰에 따라, P=NP임을 증명한 것이다. 관심이 있으시다면 세상에 어떠한 NP-complete 문제들이 있는지 한번 조사해 보시고, 증명에 도전하시길... 단, 존 내시처럼 정신분열로 고생하시지는 마시길 ^