강력

강력을 제대로 몇 가지를 더 얘기해야 한다. 이미, SU(3)의 대수적 구조, flavour/color 대수에 대해서 상세히 얘기했으니 남은 것은 게이지 대칭성에 따른 QCD입자들의 운동 방정식을 위한 QCD 라그랑지안에 대한 설명과 Feynman diagram에 따른 입자들간의 상호 작용에 관한 정확한 수학적 묘사일 것이다. QCD 라그랑지안에 대해서만 이번 포스팅에서 간단히 설명하고 후자는 시간이 되면 나중에 하거나, 오늘로 표준 모형에 관한 정리를 마무리하고자 한다. 표준 모형 SM에 대해서 실체적 진실인 것처럼 믿을 이유는 전혀 없다. SM이 완벽하지 않음은 물론, 그것이 본질과 일치하지 않을 가능성이 있음을 이미 많은 물리학자들은 알고 있다.

 

입자물리의 이해에는 게이지 이론, local gauge transform의 이해가 필요하다. 게이지 대칭성은 사실 Hilbert 공간에서의 회전 대칭성이다. 전역 global symmetry가 존재하고, 국지적인 local gauge symmetry가 존재한다. 어떤 지점에서 어느 방향을 보더라도 물리현상은 대칭이다. 전역대칭은 자연스럽다. 그러나, 이 지점에서는 10도 방향을 보고, 그 옆 지점에서는 11도 방향을 바라봐도 물리현상이 대칭일 이유는 없을 것이다. 비 자연스럽다. Local gauge symmetry는 우리가 자연을 기술하는 방정식의 redundant degrees of freedom때문에 생긴다. 즉, 자연을 기술하는 방법이 다양하게 존재하기 때문이다.

 

QCD lagrangian은 다음과 같이 주어진다. 형태적으로는 QED와 매우 유사하다. 그러나, non-Abellian group이기 때문에 그 세부는 QED와 확연하게 다르다. 아래 수식에서 왼쪽 항이, 그 유명한 Dirac equation이다. 세상에 존재하는 Fermion 입자들은 bispinor space (4x1 complex space), 왼손잡이와 오른손잡이를 함께 기술해야 한다. 그리고 입자와 반입자의 운동도 함께 기술된다. 원래, Dirac의 의도는 그냥 단순히 상대론적인 입자의 운동을 설명하고자 하였으나, 그는 본의아니게 물리학을 심오한 추상의 세계로 이끈다. 두번째 항은 gauge boson field의 운동 에너지에 관한 항이다.

 

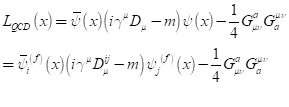
SU(3)공간에서의 게이지 변환은 다음 수식으로 주어진다. 아래에서 첨자 a는 gluon boson의index로 1부터 8까지 값을 가진다. Exp(ix)~(1+ix)로 근사화하는 것을 infinitesimal transform이라고 부르고, 이것이 SU(3)와 su(3) lie algebra를 연결짓는 부분이다. 그리고, T_a행렬을 SU(3) 그룹의 generator라고 부른다. Color 공간에서 가능한 8가지의 회전 방향을 표현한다.

 

QED의 경우는 U(1)대칭성을 표현하기 위한 1개의 boson field만 필요하다. Photon, 빛이다. 그러나, QCD를 표현하기 위해서는 8개의 boson field가 필요하다. 글루온이라고 부르는 입자들이다. 위의 식에서 가장 마지막 가환 관계가 0이 아니기 때문에 비가환(non-Abellian) 대수라고 부르며, 요 간단한 사실 때문에 QCD가 다른 모든 힘과 다른 성질을 드러낸다.

 

 

Local gauge 변환을 하면 단순 편미분 연산자로 미분하면 원래의 라그랑지안과 동일하지 않다. 일반 상대성이론에서 한 지점의 벡터와 다른 지점의 벡터를 비교하기 위해서, 다른 지점의 벡터를 현재지점으로 parallel transport해야 한다. 요렇게 두 지점의 벡터의 차이를 계산하여 미분하는 것을 공변 미분 (covariant derivative)라고 부른다. 게이지이론에서는 편미분 연산자 대신 공변 미분 연산자를 사용해야 한다. 그런데, QCD의 경우, 이 공변 미분 연산자의 변환룰이 QED에 비해서 오묘하다. 비가환연산자이기 때문이다.

 

위의 과정은 사실 QED과정과 거의 동일하다. 게이지 대칭성을 위해서 U(1) boson field가 필요했고, U(1) boson field 의 dynamics가 바로 전자기력, Electromagnetic force를 가져온다. 위에서도 동일하게 게이지 대칭성을 위하여 8개의 SU(3) boson field가 존재해야 하며, 그 boson field가 QCD, color force를 가져온다. 아래 그림과 같이, 그 단순한 수학적 구조 때문에 gluon 상호 작용이 생기고, gluon이 color charge를 가진다.

 

이미 설명한데로 SU(3)의 비가환 성질 때문에, 그 대수적 구조 때문에 Gluon 입자들 사이에 비선형적인 결합항이 발생한다. 다른 말로는 gluon boson 입자들이 charge를 가지기 때문에 그들 간에 color 를 매개로 한 상호 작용항이 발생한다. 요 상호 작용항은 beta함수의 부호를 바꾸게 되고, Beta함수의 부호가 바뀌게 되면 vacuum screening의 방향성이 달라진다. 요기에 대해서 간단히 얘기해 보자. 이와 관련한 재미있는 일화가 있으나, 다음 기회로 넘긴다. 2004년 노벨상 수상에 관한 흥미로운 얘기이다.

 

우리 눈에 아무것도 없는 것처럼 보이는 공간은 실제로는 무엇인가로 꽉 차 있는 공간이다. 몇 년전 Einstein 의 생일에 전세계 저명 물리학자들이 모여서 토론한 주제가 “The existence of nothing”이었다. 사실 말이 되지 않는 명제이다. 무의 존재라.. 존재가 없는 것을 무리가 얘기하는데, 우리는 존재하는 무를 얘기하고자 하다니… 어쨌던, 그 때 말하는 무는 정확히는 vacuum을 얘기한다.

 

양자장론에서 vacuum은 입자가 없는 상태이지만, 아무것도 없는 상태는 아니다. 우주는 한번도 아무것도 없었던 적이 없다. 있는 것은 있고, 없는 것은 없다는 파르메니데스의 명제는 단순하면서도 심오하다. 양자장론에서 진공 상태는 우주에 가득 차 있는 quantum field가 가장 낮은 에너지 레벨에서 불확정성의 원리에 따라 진공 요동을 치고 있는 상태를 의미한다.

 

Quantum fluctuation은 많은 현상을 일으킨다. 간단히는 전자와 양전자를 끊임없이 만든다. 무수히 많은 virtual particle은 전하의 particle에 의해서 polarization 현상, 분극현상을 만든다. +charge 주위로 -charge들이 접근하여 원래 charge의 양을 그것보다 작은 것처럼 보이게 한다. Virtual particle의 양이, point particle에서 벗어나면 날수록 많기에, screening effect도 커진다. 우리가 관측하는 전하의 양은 충분히 점전하로부터 멀어진 점에서 측정한 값이며, 점전하에 가까이 접근하면 할수록 그 값은 커진다. 아래 강의자료를 이해할 수 있다면 내 말을 이해한 것이다.

 

QCD에서도 마찬가지이다. 진공에서 quark와 anti-quark, gluon들이 끊임없이 진공에서 생겨난다. 그들은 color charge를 가지고 있기에 quark의 주위에 그들은 몰려든다. 그러나, beta function 의 값이 음수가 될 수 있다는 사실 때문에, 근본적으로는 Gluon 의 수학적 구조가 비가환 SU(3) 군이라는 성질 때문에, 이번에는 반대로 anti-screening 현상을 보인다. 즉, 점전하 쿼크에 가까이 갈수록 color charge가 사라지는 것처럼 보이는 현상이다. 아래 강의 자료를 참조하시기 바란다.

 

이 모든 현상의 결과는 quark는 아주 좁은 공간, 고에너지 물리세계에서는 서로 간에 끌리는 힘이 없이 자유로운 입자인것처럼 행동한다. Asymptotic freedom이라고 부른다. 이제, 그들 사이의 거리가 멀어지면, 강력한 color charge와 gluon 장들은 그들을 단단한 끈으로 묶어둔다. 이전 포스팅에서 얘기한 flux tube현상에 의해서이다. 아래 좌측 그림처럼 전자기장은 두 전하 사이에 모든 방향으로 field가 골고루 퍼져나감에 비해서, gluon field는 두 전하 사이에 끈처럼 1차원적으로 tube를 형성하여, 거리가 멀어져도 그 힘의 밀도가 약해지지 않는다. 그래서 우리는 절대로 단일 quark와 단일 gluon을 볼수 없는 것이라고 물리학자들이 설명한다.