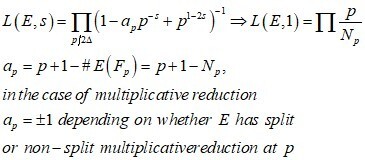수학이론
Birch and Swinerton-Dyer 문제
existence_of_nothing
2022. 7. 30. 17:17
타원 곡선 위의 유리수 해의 개수는 몇 개나 될까? 일단 두 유리수 점, P와 Q를 구하고, 타원곡선의 대수 방법 즉, P+Q는 두 점을 이은 선과 타원의 다른 점과의 교점 R을 x축에 대해서 대칭시킨 점, 즉 -R을 구하면 되는데, 두 점이 유리수일 경우, 기울기도 유리수이고, 그 직선위에 있기에 당연히 P+Q점도 유리수이다. 이제, R점과 다시 Q점을 잡아서 R+Q를 연결해서 새로운 점을 찾고, 이렇게 계속하면 무한개의 점들이 나올 것 아닐까?
문제는, R=P+Q, W=Q+R=P+2Q, W+Q=P+3Q,.. 이렇게 진행하다보면 nP=0이 되는 경우가 발생한다는 것이다. 이러한 n을 P의 차수(order)라고 부른다. 차수가 유한한 원소를 torsion element라고 부르고, 이렇게 finite order torsion element들로 그룹을 이루면 이것이 torsion subgroup이 된다.
모델 베유 정리는 아벨 다양체 위에 존재하는 유리수 해들의 집합들이 모두 유한개의 생성원들로 만들어진다는 내용이다. “Abelian variety A over a number field K, the group A(K) of K-rational points of A is finitely generated abelian group, called the Mordell-Weil group. When A is E and K is Q, it is a Mordell’s theorem.”
1901년 Poincare가 처음으로 그 내용을 얘기하고, 1922년 Louis Mordell이 Elliptic curve에 대해서, 1929년 Weil이 박사학위 논문으로 일반적인 모든 A, K에 대해서 성립함을 증명하여 그 이름이 모델 베유 정리이다. 유리수 해들의 집합이 유한 가환 군으로 구성되기에, fundamental theorem of finitely generated abelian group 이론에 따라, 타원 곡선위의 유리수 점들은 다음과 같이 표현할 수 있다.
문제는, R=P+Q, W=Q+R=P+2Q, W+Q=P+3Q,.. 이렇게 진행하다보면 nP=0이 되는 경우가 발생한다는 것이다. 이러한 n을 P의 차수(order)라고 부른다. 차수가 유한한 원소를 torsion element라고 부르고, 이렇게 finite order torsion element들로 그룹을 이루면 이것이 torsion subgroup이 된다.
모델 베유 정리는 아벨 다양체 위에 존재하는 유리수 해들의 집합들이 모두 유한개의 생성원들로 만들어진다는 내용이다. “Abelian variety A over a number field K, the group A(K) of K-rational points of A is finitely generated abelian group, called the Mordell-Weil group. When A is E and K is Q, it is a Mordell’s theorem.”
1901년 Poincare가 처음으로 그 내용을 얘기하고, 1922년 Louis Mordell이 Elliptic curve에 대해서, 1929년 Weil이 박사학위 논문으로 일반적인 모든 A, K에 대해서 성립함을 증명하여 그 이름이 모델 베유 정리이다. 유리수 해들의 집합이 유한 가환 군으로 구성되기에, fundamental theorem of finitely generated abelian group 이론에 따라, 타원 곡선위의 유리수 점들은 다음과 같이 표현할 수 있다.
이제, 관심이 있는 것은 E(Q)의 rank r은 얼마이고, 어떻게 구하느냐일 것이다. 이 문제는 생각보다 훨씬 복잡하여 현재까지도 open problem인 Millennium problem의 하나인 “Birch and Swinnerton-Dyer conjecture”로 남아있다. 두번째 관심은 위에서 제외된 F, torsion grup의 element의 수가 무한개이냐 유한개이냐, 유한개라면 어떤 것들이냐일 것이다.
=======================
1908년 Beppo Levi는 수많은 타원곡선들을 연구하여 1911년 다음과 같은 torsion conjecture 혹은 Ogg conjecture(1971)를 발표한다. 그 내용은 타원곡선위의 torsion 그룹은 다음과 같은 종류만이 가능할 것이라는 추측이며 1978년 수학자 Barry Mazur가 증명하여 Mazur theorem으로 알려져 있다.
=======================
1908년 Beppo Levi는 수많은 타원곡선들을 연구하여 1911년 다음과 같은 torsion conjecture 혹은 Ogg conjecture(1971)를 발표한다. 그 내용은 타원곡선위의 torsion 그룹은 다음과 같은 종류만이 가능할 것이라는 추측이며 1978년 수학자 Barry Mazur가 증명하여 Mazur theorem으로 알려져 있다.
그러한 torsion group을 찾는 방법 중 하나는 다음과 같은 Lutz-Nagell theorem (1935, 1937) 이 알려져 있다. 아래 방법에 따라 torsion group을 비교적 쉽게 찾을 수 있다.
예를 들어, 타원곡선 y^2=x^3+1 의 판별식=27이므로 정수 중 y^2이 27을 나누는 값은 +-1,+-3밖에 없다. 따라서 {(0,-1), (0,1)} 이 3-torsion point들이고 {(2,3)(2,-3)} 이 6 torsion point들이다. 그 외에는 없다.
======================
타원 곡선위의 모든 점들은 유한 가환 군이고(Mordell-Weil theorem), 그 중, finitely generated 되는 그룹 F의 성질은 정확히 알려져 있고(torsion conjecture, Mazur theorem) 실제로 어떻게 구하는지도 알고 있다(Lutz-Nagell theorem). 그러나, 군의 rank를 구하는 문제는 앞서 얘기한 데로 여전히 미해결 문제이며 클레이 연구소의 100만불 문제 중 하나이다.
1960년대에 Peter Swinnerton-Dyer는 영국 캠브리지 대학에서 컴퓨터로 Fp상에서 정의된 타원곡선위의 점들의 수 Np를 계산하였다. 다양한 곡선위의 점들을 계산하던 중, 그들은 타원곡선의 rank r과 Np 사이에 다음과 같은 점근적 관계가 있음을 발견하였다. 처음에는 우연한 발견인 줄 알았지만, 점점 더 데이터가 증가함에 따라, 그것이 일종의 법칙인 것처럼 인식되었다.
======================
타원 곡선위의 모든 점들은 유한 가환 군이고(Mordell-Weil theorem), 그 중, finitely generated 되는 그룹 F의 성질은 정확히 알려져 있고(torsion conjecture, Mazur theorem) 실제로 어떻게 구하는지도 알고 있다(Lutz-Nagell theorem). 그러나, 군의 rank를 구하는 문제는 앞서 얘기한 데로 여전히 미해결 문제이며 클레이 연구소의 100만불 문제 중 하나이다.
1960년대에 Peter Swinnerton-Dyer는 영국 캠브리지 대학에서 컴퓨터로 Fp상에서 정의된 타원곡선위의 점들의 수 Np를 계산하였다. 다양한 곡선위의 점들을 계산하던 중, 그들은 타원곡선의 rank r과 Np 사이에 다음과 같은 점근적 관계가 있음을 발견하였다. 처음에는 우연한 발견인 줄 알았지만, 점점 더 데이터가 증가함에 따라, 그것이 일종의 법칙인 것처럼 인식되었다.
이제 L-series 를 다음과 같이 정의한다. 아래 함수에서 s는 복소수이며, E는 타원곡선을 의미하며 delta는 판별식, p는 소수를 의미하며 아래 수열은 Re(s)>3/2에서 수렴함이 알려져 있다. 아래에서 보듯이 L(E,1)이 바로 앞서의 그 실험적 공식의 역수에 해당한다. 따라서, 그들은 L(E,s)가 E(Q)의 rank와 어떠한 관련이 있지 않을까라고 추측을 시작한다.
100만불 짜리 문제의 마지막 형태는 아래의 수식으로 정리되는 Birch and Swinnerton-Dyer 추측이다. 2년만 늦게 증명했더라면 페르마 정리가 100만 불 문제에 들어가서 와일스 교수가 수상했을 것이라는 농담을 수학자들이 한다. 와일스는 그러나, 100만불 문제 출제위원으로 섭외되어 아래의 문제를 제시하는 영광을 가진다. 물론 출제료도 두둑히 ^^
이 문제의 의미는 타원곡선 상의 유리수 점들이 이루는 군의 rank는 L(E,1)상의 (s-1)항의 차수와 동일하다는 것으로 유리수 점들이 이루는 군에 대한 마지막 퍼즐을 푸는 것에 있다. 2021년 현재까지 몇가지 특수한 경우에 대해서는 증명되어 있지만, 일반적인 경우에 대해서는 갈 길이 요원한 상태이다.
반응형