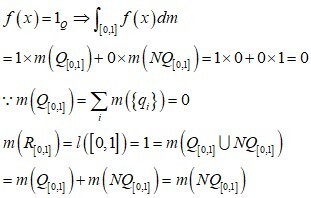측정이론

=====================

Derichlet 함수는 유리수일때 1, 무리수일때 0인 함수이다.

• 

이 함수는 적분이 가능한가? 라는 질문을 던질 수 있다. 먼저 밑변을 잘게 쪼개고, 높이를 곱하고.. 하려고 하니 문제에 부딪힌다. 왜냐하면 아무리 잘게 쪼개도 그 구간에는 무한한 갯수의 유리수점과 무리수점들이 존재하기 때문에 높이란 것을 어떻게 잡아야 할지 결정할 수 없기 때문이다. 이것을 수학적으로 그 함수는 Rieman integral 하지 않다고 얘기한다 (monotone convergence theorem, MCT가 성립하지 않은 대표적인 예로 해석학 책에 소개된다).

그러면 이 함수를 적분할 수 있는 방법은 없을까? 프랑스 수학자 앙리 레옹 르벡(Henri Leon Lebesgue, 1875~1941)은 적분에 관한(혹은 길이,넓이, 부피에 대한) 개념을 다시 새롭게 원점에서 부터 재정의하여 그 함수를 적분 가능하게 하는 Lebesgue integral을 제시한다.

리만 적분에서는 어떤 함수 f(x)를 밑변을 잘게 쪼개서 그 높이를 곱하는 방법 즉,

• 

와 같이 적분을 정의한다. 이 정의에 따라 앞서 얘기한 Derichlet function을 적분하려고 하면 문제에 부딪힌다. 우리가 생각하는 적분의 개념으로는 이 문제를 해결하기가 어렵다. 뭔가 새로운 패러다임이 필요한 것이다.

이를 위해서 Lebesgue는 먼저, 가장 간단한 interval의 길이로 부터 시작해서 다음과 같이 정의되는 Lebesgue outer measure를 정의한다. 이 논리를 R^n, n차원 유클리드 공간으로 확장하면 넓이, 부피의 개념도 같이 정의할 수 있다.

• 

Lebesgue는 아래와 같이 정의되는 inner measure도 함께 정의하였지만, 대부분의 경우에는 inner와 outer measure는 동일하며, 오늘날은 outer measure를 Lebesgue measure라고 부른다. 그 둘이 동일할 때, 그 집합 A가 Lebesgue measurable하다고 정의한다.

• 

만약 어떤 집합이 countable하다면, 즉, 그 집합의 원소들에 자연수를 1:1로 대응시킬수 있다면 그러한 집합의 measure는 각각 element들의 Lebesgue measure들의 합과 동일한다.

• 

Lebesgue integral, probability theory에서 아래와 같은 sigma algebra 얘기를 많이 듣는다. 이것은 우리가 측정할 수 있는 모든 집합들을 모아 놓은 집합이며, 그 안에서 우리는 measurable인지 아닌지를 고민할 필요없이, 자유롭게 measure에 대해서, 적분과 확률에 대해서 논의할 수 있다. (X, ∑=S, m)가 모두 정의될 때 그러한 공간을 measure space, 측도 공간이라고 부른다.

• 

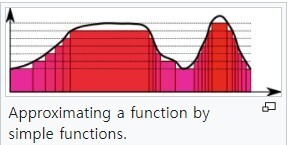
Lebesgue integral을 정의하기 위하여 먼저, 다음과 같은 simple function을 정의한다. Riemann integral의 step function에 해당하는 함수라고 생각하면 된다. 그리고, simple function에 대한 Lebesgue integral을 아래와 같이 정의한다. Rieman integral의 밑변의 길이에 해당하는 것이 measure이고, 높이에 해당하는 값이 아래에서 a_i에 해당한다. 다음 스토리는 뻔할 것이다. 이제, 어떤 일반적인 함수를 어떤 구간 혹은 집합에 대해서 적분하려면, 그 구간/집합을 measurable set들로 잘게 쪼개고, 그 measurable에서의 함수값을 곱하여 더하면 될 것이다.

• 

이후로도 많은 얘기를 해야 하지만, 체력이 딸리는 관계로, 여기서 마무리하자. 이제 아래와 같이, 함수 f를 f+와 f-함수로 분리하여 표현하고, 그들에 대해서 Lebesgue integral을 simple function의 최대값(sup)으로 표현한 후, 그 차이를 빼는 형태로 정의한다.

• 

Lebesgue integral과 Riemann integral의 차이에 대한 약간의 감을 가지려면 아래 그림을 이해하면 된다. 종래의 Riemann 적분은 x축을 일정한 간격으로 잘게 쪼개는데 반해서, Lebesgue integral은 반대로 Y축을 일정한 간격으로 쪼개고, 그 간격에 해당하는 여러 x들의 집합들에 대한 measure를 곱한다고 생각하면 된다.

• 

이제, 원래의 문제로 돌아가서, Derichlet function의 Lebesgue 적분값은 얼마일까? 아래와 같은 간단한 과정에 따라 그 값은 0이다.

•