액체상태의 물질, 생명

우주에서 액체 상태의 물질을 발견하기란 쉽지 않다. 항성의 내부는 주로 플라즈마 상태이고, 대부분의 행성은 고체 상태의 물질들로 이루어져 있다. 물질들은 온도가 높으면 기체 상태로, 너무 낮으면 고체 상태에 머문다. 고체 상태는 continuous symmetry 가 discrete symmetry 상태로 변한 상태이고, 그 대칭 파괴의 형상에 따라 다양한 물질들이 생성된다.

 

액체는 continuous symmetry를 유지하지만, 분자들간의 거리가 고체에 가깝기에 고정된 부피가 존재한다. 온도가 높은 상태에서 자유도를 누리던 분자들이 온도가 내려가면 추위를 견디지 못하고 스스로 뭉친다. 어떤 원리로 그들은 하나로 뭉치게 된 것일까?

 

통계 역학의 처음은 기체 상태, 이상 기체의 PVT가 주어진 경우의 평형상태에 대한 연구부터 시작한다. PV=nkT, 고등학교에 배운 어떠한 공식보다도 생생하게 기억이 나는 공식 중 하나이다. 이것은 PV=constant라는 보일의 발견과, V/T=constant라는 샤를의 법칙이 합쳐진 공식이다. 기체 상태에서 압력을 증가키면 부피가 감소하고, 반대로 감소시키면 부피가 증가한다. 부피가 동일한 상태에서 압력이 낮아지면 온도가 내려가고 이것이 냉장고의 동작 원리이다.

 

통계역학의 처음은 이렇게 서로 상호 작용이 없는, 독립적인 수많은 입자들로 이루어진 세상에서 평형 상태에 나타나는 여러 거시 변수들, 온도, 압력, 부피 등에 대해서 얘기하고, 그러한 거시 상태를 만들어 낼 수 있는 미시 상태의 수, 엔트로피라는 개념 도출과 정량적 계산 방법을 주로 얘기한다. 그러나 좀 더 진도가 나가면 입자들 간의 상호 작용이 있을 때 나타나는 다양한 현상들, 대표적으로 상 변이, phase change에 대해서 얘기한다.

 

원자는 작다. 그냥 작은게 아니라 무지무지 작다. 단 1몰에 존재하는 입자의 수가 10^23개 정도이다. 은하수 전체에 존재하는 모든 별들의 수가 10^11개 밖에 되지 않고, 가시 거리의 우주 내에 존재하는 항성 전체의 수, 우주의 별의 수가 10^22개 정도로 추정되니, 원자가 얼마나 작은지, 존재들이 얼마나 깨알들로 이루어져 있는지 알 수 있다. 이러한 극미의 존재들이 규모를 이루면서 온갖 자연의 신비를 만들어낸다.

 

===========================

 

분자들 간에는 서로 잡아 당기는 성질이 존재한다. 이것은 왜 발생하는 것일까? 그 근본은 전자기력 때문이다. 원자나 분자가 단독으로 세상에 존재할 때에는 전하 분포가 원형 대칭의 형태 (spherically symmetry)이다. 그러나 그 둘이 만나게 되면 아래와 같이 +는 -와 가까워 지려는 반대로 -는 +쪽에 끌리기 때문에, dipole 이 생성된다. 전자기장을 공부하면 dipole moment의 정의를 배우고 dipole field에 의해서 생기는 전자기장 계산법을 배운다. 구글링하면 1시간이면 따라갈 수 있을 정도로 간단하다.

 

Monopole, 즉 charge 하나만 존재하는 경우에 V는 1/r로 E는 1/r^2으로 떨어짐은 고등학교 물리시간에 배운다. Dipole의 경우에는 전기장 E field가 1/r^3으로 좀 더 거리에 급하게 반비례해서 떨어진다. 따라서, 멀리 떨어진 존재들에게는 그 영향력이 약하다. 그러나, 존재들이 어느 정도의 거리에 접근하고, 그들의 운동에너지가 그 미미한 인력을 떨칠 수 없을 만큼 온도가 낮으면 그 힘은 큰 위력을 발휘한다. 이것을 반데르발스 (Vander Waals) 힘이라고 부른다.

 

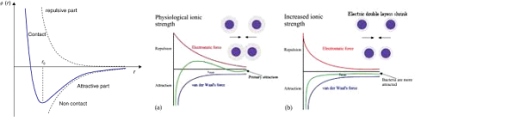
Vander waals force는 하나의 dipole field가 인접한 분자를 다시 dipole 화 하면서 발생하기에 그 힘은 1/r^6, 거리의 6제곱에 반비례하는 근거리력이다. 그 힘에 의해서 분자들은 서서히 끌려오다가, 파울리 배타원리가 그들을 밀어내는 지점에서 가장 에너지가 낮은 상태를 이루고, 더 가까이는 접근하지 못한다. 그 정도의 거리에서 서로 뭉쳐다니는 상태가 액체 상태이다. 지구에 액체 상태의 물질들, 특히 물이 존재하기에 생명이 피어나게 된다.

 

상호 작용이 있는 경우에는 더 이상 PV=NkT의 관계식이 유효하지 않고, 아래와 같이 고차항들이 나타나기 시작한다. 아래 식에서 B_i(T)를 Virial coefficient, 아래 전개를 Virial expansion이라고 부른다.

 

상호 작용이 존재하는 경우의 해밀턴 연산자와 partition function은 아래와 같이 주어진다. 상호 작용이 없는 경우의 partition function Z가 단순히 N개의 Independent Gaussian random variable의 곱으로 주어지기에 Z및 entropy를 쉽게 구할 수 있다.

 

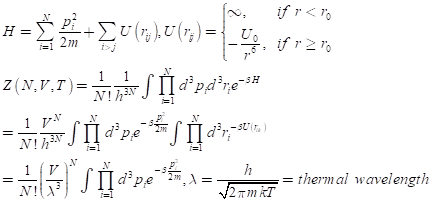
그러나, interaction이 주어지는 경우는, 간단한 potential field라도, 그 항이 exponential 항 안에 주어지기에 closed form으로 계산이 간단하지 않다. Exponential 함수를 Taylor 전개하는 방식을 이 경우에는 적용하기 어려ㅑ운데, U(r)이 r 이 0으로 수렴하는 경우에 무한대로 발산하는 형태이기 때문이다. 따라서 아래와 같은 Mayer f function함수를 사용하여 근사화하는 방법을 사용한다.  

 

위의 식에서 보듯이 PV=NkT는 분자들 간의 상호 작용이 존재하는 경우에는 더 이상 성립하지 않는다. 이제 입자들이 수축하는 방향으로 작용할지, 아니면 도리어 팽창하는 방향으로 작용할지는 위의 식의 적분값에 의해서 결정될 것이다. 만약 U(r)>0이면, f=exp(-beta U)-1<0 이고, 압력은 증가할 것이다. 그러나 U(r)<0이면 f(r)>0이고 적분값은 양수가 되어서 인력으로 작용할 것이다. 액체 상태에 접근하는 것이다. 이제 앞서 주어진 potential에 대해서 위의 값을 구해보면

 

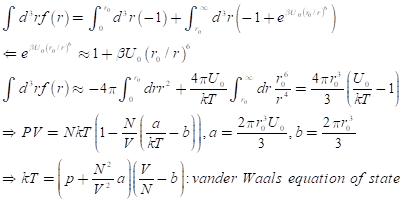
위의 복잡한 수식들이, 고등학교때, 분자들을 모으는 약한 힘, 반데르 발스 힘이라고 배운 것이다. 그 밑바탕에는 전자기력이 있다. 우주는 존재들을 중력의 힘으로 한 곳에 모으고, 음과 양의 조화로 존재들을 결합한다. 존재들에게 에너지가 주어지면 자유를 누리다가, 에너지를 가져가면 약한 dipole field에도 저항을 못하고 꾸물꾸물 모여서 무리지어 흘러다니는 액체 상태가 된다. 이러한 액체 상태가 존재하기에 물질들은 순환을 하고, 생명들이 피어난다.