수성 근일점 문제

뉴턴의 magnum opus, “Philosophiae Naturalis Principia Mathematica”가 1687년에 publish 된 후, 그 이 후의 세상은 그 전 세상과 질적으로 다른 사회에 진입한다. 케플러의 법칙이 단순 관측 법칙이 아닌, 아름다운 수학에 의해서 정확히, 한치의 오차도 없이 기술될 수 있다는 것은 그 당시 사회에는 충격 그 자체였다.

 

어쨌던, 뉴턴 이후에 수많은 천문학자들이 뉴턴의 법칙을 적용하여 행성의 궤도를 정확히 구하고 관측으로 이를 확인하고자 노력하였다. 뉴턴의 법칙을 적용하려면 태양과 행성 하나 사이의 인력이 아닌, 다른 모든 주요 행성들의 인력을 모두 고려하여야 하였고, 그 계산이, 오늘날에야 컴퓨터 프로그래밍으로 금방 계산 할 수 있지만, 그 당시는 인간이 모두 일일이 계산을 수행해야 했기에 엄청난 일이었지만, 천문학자들은 그 일을 수행하였다.

 

1757년 핼리는, 방문때마다 불운을 가져온다는 핼리 해성의 궤도를 발표하였고, 1757년 Alexis Claude Clairault라라는 천문학자는 조수 2명의 도움으로, 목성과 토성의 인력까지 고려하여 꼼꼼히 계산하여 1759년 4월에 다시 방문하리라고 예측하였고 실제로 (33일 정도 일찍 도착했지만) 혜성이 나타났다. 1781년에는 고대이후 처음으로 천왕성(Uranus)을 발견하는 성과도 달성한다. (천왕성:1781, 해왕성:1846, 명왕성: 1930 발견).

 

1845년 Le Verriere(르베리에)라는 천문학자가 천왕성의 궤도를 계산한 결과 예상된 궤도와 다르게 공전함을 발견하고, 천왕성의 바깥에 또다른 행성이 존재할 것이라고 예측하고 그 위치를 추정하고, 실제로 베를린 천문대에서 해왕성(Neptune)을 발견함으로써, 뉴턴의 만유 인력 법칙은 절대 만능의 도구로 등장한다. 르베리에는 해왕성 문제를 해결한 후, 수성의 정확한 궤도를 찾는 문제를 연구한다.

 

태양과 행성, 2body만 존재한다면 행성이 태양의 주변을 한바퀴 돌면, 공전 주기 후에 정확히 원래 시작한 지점에 돌아올 것이다. 그래야 타원 궤도가 완성되기 때문이다. 그러나, 주변의 행성들도 인력을 미치고, 그들의 공전주기가 모두 다르기 때문에, 행성의 공전 주기마다 정확히 같은 곳에 도달하지 않는다. 이러한 과정을 여러 번 거치게 되어, 오랜 시간이 지나면 다시 원래의 위치로 돌아온다.

 

수성의 경우 이러한 영향으로 근일점의 세차 현상 (Precession of the Perihelion of Mercury)이 발생한다. 르베리에가 주변의 모든 행성의 인력까지 고려한 수성의 세차운동을 계산하니 100년마다 5599초가 이동한다고 알려져있다. 이중 5025초는 지구지축의 세차효과에 의한 착시현상이고, 타 행성들의 중력 효과로는 531초 (초가 1/3600도)가 틀어져야 하는데, 실제로 관측값은 이보다 43초가 더 큰 574초로 나타났다.

 

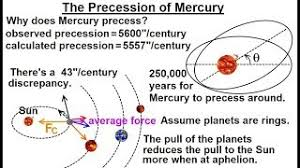
천왕성의 경우와 마찬가지로 르베리에는 태양과 수성 사이에 미지의 행성이 있을 것이라고 예측하고 그 이름을 Vulcan이라고 명명하였다. 천문학자들이 Vulcan찾아 3만리를 떠나고 실제로 1859년에 수성을 Vulcan으로 혼동하는 에피소드까지 생겼지만, 끝내 Vulcan을 발견하지 못하고, 뉴턴 법칙이 정확하지 않은 것은 아닌지 의심하기 시작한다.

 

실제로 뉴턴 법칙에서 거리에 반비례하는 항을 거리의 역제곱 즉 1/r^2이 아니라 1/r^(2+0.00...)로도 세차 운동의 설명이 가능하다는 논문이 발표된다. 이 차이에 대한 정확한 설명은, 아인슈타인의 일반 상대성이론이 등장하고야 가능해진다. 

 

인간들이 우주의 본질을 알기는 어렵다. 그러나, 현상들을 설명하는 것은 가능하며, 그 설명방법이 한가지만 있는 것은 아니다. 일반 상대성 이론의 설명에 따라 수성 근일점 문제가 설명되지만, 오늘날에도 뉴턴 역학의 수정 혹은 우리가 모르는 암흑 에너지 등 다양한 방법으로 현상을 설명하는 논문들이 발표되고 있다.