알콰리즈미, 알고리듬이라는 이름의 아랍 수학자

알고리듬(Algorithm).. 일단 어감부터 영어 같지가 않다. 알고리듬은 알콰리즈미(780-847)라는 페르시아 수학자에게서 유래한다. 그의 이름을 라틴어화한 algorismus에서 따온 말이다. 그는 또한 대수학(algebra)이란 용어도 만들었다. Al-jabr(알자브르)라는 2차 방정식 해법 중 하나에서 나온 용어이다(al-jabr wa al-muqabala, 알자브르 왈 무카발라). 이전 포스팅의 디오판토스와 더불어 대수학의 아버지로 불린다. 또한 프톨레마이오스의 삼각함수를 소개/발전한다.

 

632년 무하마드가 사망하고 칼리파 시대를 연다. 4대 칼리파 알리의 암살(661년)을 두고 시아파와 수니파가 갈라지고 우마이야 왕조, 압바스 왕조를 이루며 이슬람 문화가 융성해진다. 그러나 많은 학자들이 연구하던 “지혜의 집”(알렉산더리아도서관 같은 대형 도서관, 바그다드)에 1285년 야만족 몽골이 침략하여 수많은 책들을 티그리스 강에 버려서 또 한번 과학의 진보를 방해한다.

 

알자브르는 양변에 동일한 수를 더해서 음수를 제거하는 방법이다. x-5=2 일때, 같은 수 5를 양변에 더해서 음수 5를 없앤다. 현대적인 용어로는 이항이라고 부른다. 이슬람 수학자들은 인도와 달리 음수의 개념을 인정하지 않았다. 디오판토스와 알자브르 모두 음수의 답은 인정하지 않고, 계수도 양수만 고려하였다.

 

오마르 하이얌(1048-1131)은 페르시아 수학/천문학자/시인이다. 그의 시 루바이야트는 19세기 피츠제럴드(1809-1883, 다윈과 동시대)가 의역하면서 유명해진다. 루바이야트의 시구는 삶의 본질인 허무에 대해서, 찰나의 반짝임 뿐인 인생을 관조하는 4행시이다. 하이얌은 1070년 “대수학 문제들에 관한 시연 논문”으로 명성을 얻는다. 3차 혹은 고차 방정식의 해법을 연구하고 유클리드의 평행선 공리에 의문을 제기하여 800년 전에 비유클리드 기하학에 대한 생각을 한다.

 

기하학이 일찍부터 현대 수준으로 발전함에 비해 정수론, 대수학은 그 발전속도가 그렇게 빠르지는 않다. 물론 기하학과 달리 직관적이지 않고 추상적인 수를 다루는 학문상의 어려움도 있었겠지만, 0과 음수를 숫자에 포함하지 않은 고정 관념도 그 원인일 것이다. 아라비아 혹은 인도-아라비아 숫자는 중세에 이슬람 수학에 도입된다. 최초로 도입한 이는 모르지만 기록상으로는 976년 비킬라우스 코덱스에 처음으로 언급되어 있다. 오늘날과 같은 아라비아 숫자는 아래에서 보듯이 17세기에 되어서야 완성된다. 인도에서 아주 오래전부터 사용된 0도 15세기에 와서야 비로소 하나의 문자 취급을 받는다.

 

 

숫자 0이 15세기까지 문자 취급을 못 받았으니 하물며 음수는 물론이다. 서양에서의 음수는 16세기 카르다노에 의해서 그 정당성이 인정된다. 그 반면 인도에서는 브라마굽타(598-668)가 음수를 사용하여 산술연산을 한다. 알 콰리즈미는 그리스인들의 기하학의 영향으로 끝내 음수의 도입을 거부한다. 이미 다 존재를 알고 있었지만 피하고 있었던 음수는 카르다노가 방정식의 해로서 엄연히 존재함을 지적한다. (그는 자신이 죽는 날짜를 예언하고 그 예언을 실현하기 위해서 단식으로 정확히 그 날짜에 자살했다고 한다. 똘똘하신 분이 심한 관종인 듯 하다 ㅠㅠ. )  

 

그러나, 음수의 존재를 인정하자 곧 x^2+1=0, 즉 제곱해서 음이 되는 숫자를 만나게 된다. “이 뭐꼬…” 어쨌던 카르다노는 허수도 발견하고 훗날 데카르트는 이것을 상상의 수 (imaginary number) 허수라고 부르고(사실 조롱의 의미가 크다. 이것을 수라고.. 걍 상상의 수라고 하자..) 오일러(1707-1783)은 i라는 기호를 부여한다. 그러나 사실 그 전에 누구나 음수와 허수의 존재는 알고는 있었지만, 그것이 기하학적인 어떤 관련성도 없기에 무시한 것일 뿐이다. 존 월리스(John Wallis 1673-1703) 라는 영국 수학자는 허수를 평면에 수직인 어떤 수라고 얘기한다. 비슷한 시기에 Wessel(1745-1818)이라는 노르웨이 수학자가 복소 평면의 아이디어를 생각한다.

 

3차 방정식의 일반해는 이탈리아의 페로(Fesso; 1465-1526)가 최초로 발견하고 그 후 16세기 타르탈리아 (Targaglia;1499-1557)가 재발견하지만 비밀에 붙인다. 위에서 얘기한 의사겸수학자인 카르다노(Cardano; 1501-1576)은 비밀로 하겠다고 하고서는 비법을 전수받고는 “아르스 마그나”라는 책에 이를 까발린다 (지가 최초로 한 것도 아니면서..하고 투덜투덜하면서..). 

 

4차 방정식의 일반해는 제자인 로도비코 페라리(Ferrari;1522-1565)가 구한다. 그 후 5차 이상의 고차 방정식의 일반해를 찾고자 수백 년을 노력했지만 아벨(1802-1829)에 의해서 그 불가능성이 증명된다. 또한 갈로아(Galois; 1811-1832)는 단 5년간의 연구로 군이론을 만들어내고 이는 오늘날의 현대 대수학을 만든다.

 

================

 

음수를 얘기한 브라만 굽타는 아래와 같은 원에 내접한 사각형의 면적을 구하는 브라만 굽타 공식을 만든다. 면적은 sqrt((s-a)(s-b)(s-c)(s-d)), s=(a+b+c+d)/2 이다. 치매 예방을 위하여 아래쪽에 공식의 유도과정도 적어둔다.

 

 

비슷한 문제로 헤론의 공식도 있다. 이것은 삼각형의 세변의 길이를 알 때 면적을 구하는 공식이다. 중학교 과정에 나오는 공식이지만, cos 제 2법칙으로 증명하면, 위의 과정과 동일하다.

 

 

==============

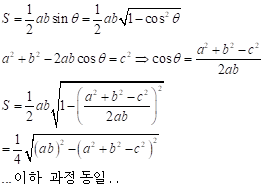
다른 몇 나라의 숫자 표기도 살펴보자.

바빌로니아

 

이집트

 

마야숫자