자신을 인식하는 물질, 존재와 의식... 자연철학적 접근
카르노 엔진 본문
고전 열역학 마지막 글이다. 이전 글에 이어서 하는 것은 아니고, 이전에 빠뜨린 부분, 카르노 엔진에 관해서 얘기한다. 학부 과정에서 배우는 것이 아마 여기정도까지가 아닐까 추측한다. 물론, 내 밥그릇이 아니라 정확히는 모른다. 이 다음부터는 Landau, Ginsburg Landau이론에 들어가면서 재규격화군 (renormalization group) 이론에 들어가고 보통은 이 분야를 SFT (statistical field theory)라고 부른다. 여기서 부터는 quantum field theory에 들어가고, 경로 적분(path integral)이 도입되며 조금 복잡한 수학적 전개가 요구되기에 학부 과정이 아니라 대학원 과정에서 다룰 것으로 추측된다.
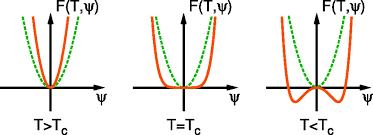
아래 그림을 보면 Tc라는 임계온도를 전후로 해서 free energy의 모양이 2차의 포물선 모양에서 4차의 멕시코 모자의 형태로 변한다. 어디서 많이 본 그림일 것이다. 그렇다 힉스 메커니즘이다. Tc이하에서는 에너지가 가장 낮은 진공 상태가 양쪽으로 2개가 존재하기에 존재들은 그 중 하나를 선택해야 하는 운명에 처한다. 이렇게 ground state에서 false vacuum 상태에서 true vacuum 상태 하나를 선택하는 과정을 SSB(spontaneous symmetry breaking)이라고 하며 그 이유 때문에 존재들은 질량을 가지고, 자석은 자화가 되고, 액체와 기체의 상이 그 온도를 중심으로 급격하게 변화한다. Landau가 하는 얘기를 미리 스포했다.
조만간 내연기관 자동차는 사라질 운명이다. 한때 아는 분이 리튬의 매장량 제한으로 전기 자동차 상용화는 이론적으로 불가능하다고 내게 얘기했었다. 그런데, 현재의 전망을 보니 그 분의 얘기는 틀린 듯 보인다. 10년 정도면 내연기관 자동차는 더 이상 생산이 안 될 가능성도 있고, 수소 자동차보다는 전기 자동차의 전망이 밝아 보인다.
어쨌던, 열 및 통계 역학을 현재 정리하고 있다. 이제 남은 주제는 Landau theory부터 시작할 것인데, 여기서부터는 statistical field theory라고 해서 학부 과정이 아니라 대학원 과정의 주제로 넘어간다. 이것을 이번에 잠깐 정리해 볼지, 혹은 잠수 후, 다음에 부상했을 때 정리할지 고민중이다. 이제까지 20개 정도의 긴 글들로 Tong 교수의 통계역학 강의록을 따라가 보았다. 다음에는 물론, 그의 SFT강의록을 쫓아갈 것인데, 사실 쉽지는 않다.
내가 좋아하는 몇몇 강의 들이 있다. 예일대학교 Shankar 교수, Mcgill 대학의 Maloney 교수, Caltech의 John preskil, Cambridge 의 Tong 교수들이 그들이다. Tong 교수의 강의는 사실 그렇게 친절하게 과정을 설명하지 않기에 이해를 위해서는 많은 노력이 필요하다. 그러나, 다양한 주제를 다루고, 역사적인 내용까지도 강의록에 포함되어 있어 흥미롭다. 물리학 분야에 Renaissance man 이 많지는 않은데, Tong 교수는 고전역학부터 초끈이론, 응집 물질 물리학까지 참으로 다양한 분야를 강의하는데 그 하나하나의 깊이가 깊음에 놀라지 않을 수 없다.
내연기관의 아이디어는 1482년 레오나르드 다빈치는 태엽으로 달리는 자동차를 설계한 그림을 남긴다. 달리기 전에 스프링을 감으면 얼마동안 그 힘으로 달릴수 있는 1인승 자동차이다.

또한 그는 1509년 화약을 터뜨려서 달리는 차를 고안한다. 1807년 프랑스 철도기관차 알퐁스 보 드 로샤가 4행정(흡입-압축-폭발-배기) 내연기관의 원리를 고안하고 1876년 아우구스트 오토는 제작에 성공한다. 이를 토대러 다임러(Daimler)와 마이바흐(maybach Benz)는 1885년 가솔린엔진을 개발한다. 그리고 1893년 루돌프 디젤이 디젤 엔진을 개발한다.

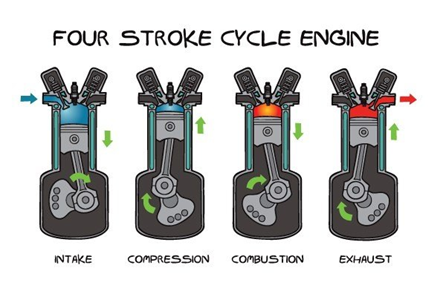
내연기관의 4행정은 intake, compression, power, exhaust의 4 단계가 1 cycle을 이룬다. 연료와 공기를 흡입(intake)하고, 고압으로 압축 후(compression), 연소하고 (power), 찌꺼기를 뱉아내면(exhaust) 하나의 사이클이 완성된다. 중학교 기술 시간에 배우고, 실습도 종종하는 내용이다.
참고로 증기기관은1705년 토머스 뉴커먼이 최초로 발명하고 1769년 Jame Watt가 성능을 개량한다. 18세기 후반 산업 혁명의 기폭제 역할은 당연히 제임스 와트의 증기관이었다. 증기기관은 내부에서 연료를 연소시키는 내연기관이 아니고 기관의 외부에서 연소를 하여 발생시킨 증기를 흡입시키는 점에서 외연기관이라는 차이점이 있다. 산업 혁명의 초기에, 사용한 연료 대비 사용 가능한 일, 즉 효율을 높이는 일은 돈과 바로 직결되는 엄청나게 중요한 연구였다. 실제로 증기기관이 처음에 제조되었을 때 열 효율은 5%에도 미치지 못할 정도로 비효율적이었다.

열역학에 관한 이론이 전무하던 시기인 1824년 사디 카르노(Sadi Carnot)는 28살의 나이에 열의 동력에 관한 고찰(Rflexions sur la puissance motrice de feu)이라는 책을 출판하지만 그의 생전에 주목을 받지 못하고 그는 36세에 콜레라로 요절한다. 그 책에서 그는 카르노 엔진이라는 이상적인 열기관의 개념을 정립한다. 카르노 엔진은 열효율이 가장 좋은 이상적인 열기관이다. 열역학을 확립하는데, 초기에는 카르노, 켈빈, 클로지우스가 크게 기여하고 이를 확률적인 해석 즉 통계역학으로 발전시키는데에는 볼츠만 깁스가 큰 기여를 한다.

===================================
통계역학 게시글 처음에, 열역학 법칙 4가지, 0~3법칙을 기술하였고, 그 중 엔트로피 증가의 법칙인 제 2법칙은 캘빈과 클로지우스의 정의 두가지가 있다고 얘기하였다.
- 켈빈의 정의:
“No process is possible whose sole effect is to extract heat from a hot reservoir and convert this entirely into work”
일은 열로 100%로 전환이 가능하지만, 반대로 열을 일로 100%로 전환하는 것은 가능하지 않다.
- 클로지우스의 정의:
“No process is possible whose sole e↵ect is the transfer of heat from a colder to hotter body”
차가운 물체에서 뜨거운 물체로 열이 흐르지 않는다.
위의 두 법칙으로부터 아래와 같은 클로지우스 엔트로피를 정의할 수 있으며, 열역학 제 2법칙에 따라 고립계 혹은 단열 시스템의 엔트로피는 절대로 감소할 수 없다는 엔트로피 증가의 법칙을 클로지우스가 보인다.

위의 두 정의는 같은 얘기를 하고 있을까? 열역학 제 2법칙의 켈빈과 클로지우스, 둘의 정의가 동일함은 카르노 엔진의 개념을 도입하여 보일 수 있다. 카르노 엔진(carnot engine)은 상태 공간에서 폐곡선을 따라 진행하는 가역 과정 (reversible process) 싸이클로 정의된다. AB간에는 등온 (isothermal) 팽창, BC간은 단열 (Adiabatic) 팽창, CD는 다시 등온 압축, DA는 단열 압축을 통해서 원래의 상태로 환원하는 싸이클이다.


AB과정에서 열 Q_H을 흡수하고, CD과정에서 열 Q_L을 방출한다. BC, DA과정에서 외부에 대해서 일을 한다. 그 일의 양은 +일 수도 있고, -일 수도 있다. 카르노 엔진의 효율은 아래와 같이 정의되며, 이것은 카르노 엔진의 종류와 무관하게 일정하며, 어떤 엔진도 카르노 엔진보다 더 높은 효율을 보일 수 없음을 증명할 수 있다.
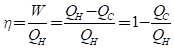
증명: 아래와 같이 비가역적인 비 카르노 엔진 Ivor을 carnot engine과 아래와 같이 연결한다. Ivor의 일을 받아서 carnot engine은 cold body에서 hot body로 열량을 이동시킨다. 그 둘을 하나의 시스템처럼 보면, composite 시스템은 외부에 대해서 아무런 일을 하지 않고 단순히, 외부에서 Q_H’-Q_H>0 만큼의 열을 받아서 Q_C’-Q_C만큼의 열을 돌려준다. W는 Ivor에서 카르노 엔진으로 온전히 전달되었으므로 Q_C’-Q_H’=Q_C-Q_H=W로 동일하다. 또한 열은 뜨거운 곳에서 차가운곳으로 이동하므로 Q_H’-Q_H>0여야 한다. 이제 Ivor의 engine 효율을 구하면

. 증명끝
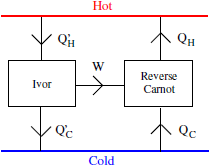
카르노 엔진의 효율이 엔진 입력과 출력 온도 차이만의 함수로 표시된다는 사실로 부터, 시스템의 온도를 카르노 엔진의 효율로 정의할 수 있다. 이상기체의 카르노 엔진 효율을 구해보자. 앞서 카르노 엔진 싸이클은 외부와의 열량 교환이 차단된 단열구간과 열량이 오고가는 등온 과정으로 구성된다. 먼저 등온 (iso-thermal)과정에서는
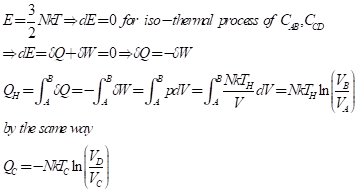
단열(adiabatic)과정에서는

위의 두 과정을 결합하여 카르노 엔진 효율을 구하면, 아래와 같이 카르노 엔진의 효율은 엔진의 동작 전후의 온도만의 함수임을 알 수 있다.
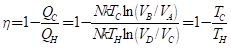
클로지우스 엔트로피는 카르노 엔진의 경우 폐경로 적분 값이 0임을 쉽게알 수 있다. 적분 경로가 복잡한 경우는 카르노 엔진의 부분합으로 표시할 수 있기에, 가역 반응의 경우 엔트로피의 적분값은 0이다. 그러나, 비가역 반응의 경우 폐구간 경로 적분을 하면 아래와 같이 0보다 작음을 알 수 있다.
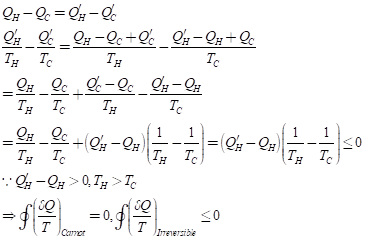
이제 아래와 같이 경로 I은 Irreversible, II는 reversible 경로로 적분을 하는 경우의 엔트로피의 변화량을 구해보면 아래와 같다.
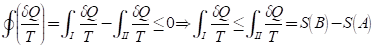
만약 열의 입출입이 없는 단열 팽창, 혹은 열적으로 고립된 시스템의 경우 엔트로피는 항상 증가한다.
'과학사' 카테고리의 다른 글
| 초기 원자 모델 (1) | 2021.09.13 |
|---|---|
| 빅히스토리 (0) | 2021.03.13 |
| 수성 근일점 문제 (0) | 2021.02.24 |
| 화성 착륙선 perserverance (0) | 2021.02.19 |
| 프랑스 혁명과 라브와지에의 죽음 (0) | 2021.02.11 |




