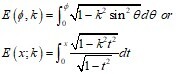타원곡선

타원 곡선 이론이 나온 배경적 지식을 한번 얘기해 보자. 이 얘기는 타원의 길이를 구하는 과정부터 시작한다.

1. 타원의 길이: 타원 적분 이론

가장 간단한 타원의 방정식은 잘 알다시피 x^2/a^2+y^2/b^2=1 이다. 장축(major axis)의 길이가 2a, 단축(minor axis)의 길이가 2b일 때의 그래프이다. 타원의 면적은 적분을 하면 쉽게 구할 수 있고, 면적은 당연히 pi x a x b이다.

• 

이제, 조금 더 어려운 문제인, 타원의 둘레의 길이를 구해 보면? Y=f(x)의 둘레의 길이를 구하는 공식은 쉽게 유추할 수 있다. 그 공식에 타원의 방정식을 대입하면.. 갈수록 복잡해진다. 결국 깔끔하게 공식이 유도되지 않고, elliptical integral이라는 꼴을 만나게 된다.

• 

타원 적분은 다양한 형태로 표시되는데, 위에서 표시한 방법 외, 다른 표현을 알아보자.

• 

위의 식은 아래와 같이도 정리된다.

• 

이것을 (complete or incomplete) elliptic integral of the 2nd kind 라고 부르고 수식으로는 아래와 같다.

• 

================================

이제 Bernoulli의 lemniscate 란 도형은 8자 모양의 궤적을 가지는 곡선이다.

• 

이 곡선의 길이를 구하면

• 

위에 나오는 적분 형태를 (complete or imcomplete) elliptic integral of the 1st kind 혹은 Legendre function of 1st kind 라고 부른다. 아래와 같은 형태의 함수이다. 앞서의 문제는 L=4aF(,pi/4,sqrt(2)) 의 형태이다.

• 

========================

이제 앞서 식으로 돌아와서, 실제의 길이를 구해 보자. Root를 바로 적분하기는 어려우니, 이항 전개를 적용하여 root항을 제거한다. 그래서 계산을 이어가면 아래와 같이 F(…)라는 hypergeometric function (초기하함수)으로 복잡하게 표현된다.

• 

위에서 F(...)를 초기하함수라고 부른다. 초기하 함수는 1655년 John Wallis가 처음으로 사용하였다. 초기하 함수는 이후 Euler, Gauss, Rieman 등 당대의 내노라는 학자들이 모두 한번식 건드린 함수이며 아래와 같이도 표현할 수 있다.

• 

위의 식이 너무 복잡하기에 1609년 Kepler는 pi(a+b)라는 근사식을 사용하였다. 1773년 Euler 는 조금 더 정확하게 2pi sqrt(a^2+b^2)/2 를, 1914년 Ramanujan은 pi ( 3(a+b) – sqrt((a+3b)(3a+b))라는 요상한 근사식을 제시하였다.

=====================

타원의 면적을 쉽게 구해서, 길이도 쉽게 구할 것으로 시작했지만, 복잡한 적분 꼴을 만나는데, 위의 마지막 꼴을 보면 분모가 제곱근안의 3차 방정식의 형태로 표시됨을 알 수 있다. 이렇게 y=sqrt(3차 방정식) 혹은 y^2+ay=x^3+bx^2+cx+d 형태로 표시되는 곡선을 그려보면 그것이 elliptic curve이다.

1655년 수학자 Wallis(1616-1703)가 타원의 길이를 구하는 과정에서 최초로 타원 적분 문제를 발표했다. 타원 적분 이론의 많은 기초적 연구는 Legendre(1752-1833)가 평생에 걸쳐 진행한다. 르장드르의 업적은 당대에는 별로 주목받지 못하다가 1827년 아벨, 그리고 자코비에 의해서 타원 곡선에 대한 연구로 이어진다. 아벨은 타원곡선 이중 주기적인 특성(double periodic property)을 발표하여, 타원곡선과 복소 moduli space간의 연결고리를 찾아내지만, 그 논문이 발표되기전 사망한다. 자코비는 타원 곡선과 정수론을 연결하는 최초의 연구를 진행하고 Jacobi theta function을 발견한다. Kal Weierstrass는 타원 곡선과 복소 모듈러 공간을 대응시키는 결정적인 함수인 Weier strass elliptic function을 찾아낸다.