자신을 인식하는 물질, 존재와 의식... 자연철학적 접근
복소수와 근의 공식 본문
아래 내용은 이과생들만 이해할 수 있는 내용이므로 복소수를 배우시지 않은 문과분들은 가볍게 skip 하시면 될 것이다. 허수(imaginary number)의 존재자체는 기원전 1세기 그리스 수학자 “헤론”도 언급할 정도로 기원전에도 이미 그 존재가 충분히 알려져 있었다. 다만 기하학적으로 의미있는 것들만 실체로 취급하는 고정관념으로 인해 오랫동안 그 존재를 무시했을 뿐이다.
이전 포스팅에서 얘기한데로 이탈리아 수학자 카르다노(1501-1576)가 삼차 방정식의 일반해를 소개한다. 잘 알다시피 이차 방정식을 풀다 보면 당연히 허수 문제에 부딪힌다. 예를 들면 x^2+1=0의 방정식의 해는 허수이다. 카르다노의 이전에는 그냥 “이 방정식의 해는 없다”라고 결론짓는다. 이러한 관념 체계 아래서는 복소수의 경우, 쌍으로 (conjugate) 해가 발생하기에 풀 수 있거나(실수 해가 존재하거나) 풀 수 없는 경우(허수 해의 존재)로 이분화 된다. 이렇게 수의 실체를 제한해 버리면, 그 추상성을 제한해 버리면 대수학의 발전은 기대하기 어렵다.
그러나, 3차 방정식의 경우 항상 실수의 해가 존재하고 때로는 conjugate pair(켤레 쌍)으로 복소수의 해가 존재한다. 따라서, 2차 방정식의 경우와 달리 어쩔 수 없이 복소수를 자주 접하게 된다. 카르다노는 이것이 자주 나타나지만 현실성이 없고 쓸데없다고 간주한다. 사실 그의 말대로 한다면 음수의 경우에도 똑 같은 문제에 부딪힌다. 예를 들면 x^2=4의 해는 +2도 -2도 된다. 왜 -2는 되고 2i는 안되는가.. 어차피 둘 다 실재하지 않는 관념적인 개념일 뿐인데? 그러나, 그는 -2는 해로 인정하면서 복소수는 끝내 거부한다.
3차 방정식 근의 공식을 살펴보자. 일단 공식 자체가 복잡하다. 이거 외워서 문제 풀면, 수능 시간 동안 한 문제 풀고 전사한다. 따라서 유도과정이 그렇게 복잡하지는 않지만, 교과서에는 소개하지 않는다.
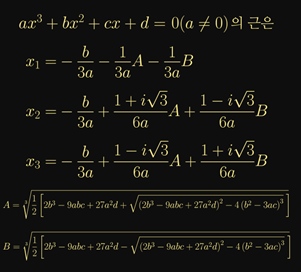
이탈리아 수학자 봄벨리(Fafael Bombelli, 1526-1572)는 카르다노의 3차 방정식의 해를 다루면서 어려운 문제에 봉착한다. x^3=15x+4 라는 방정식의 실수 해는 4임을 쉽게 알 수 있다 (그냥 대입, 어려운 용어로는 rational root theorem으로 푼다고 한다). 이것을 3차 방정식의 해의 공식에 대입하면 답이 아래와 같이 나온다. 앞서 소개한 공식의 x1에 값을 대입하면 된다.

대체 실수값의 해가 나와야 하는데, 희안하게도 복소수들의 합의 형태로 결과가 표시된다. 허수는 분명히 존재하지 않는 수라고 했는데, 그러면, 이 문제의 답은 없어야 하는데.. 4를 대입하면 답이 맞는 것은 명백하고 ..”이 뭐꼬……. “ 고민에 빠진다. 그래서, 어쩔수 없이 복소수의 연산에 대해서 생각을 하고, 복소수로 연산을 계속한다. 그 결과는 아래와 같이 원래의 해 4를 얻을 수 있다.

즉, 손꾸락/발까락으로 셀 수 있는 수만 수가 아니라, 세상에 있는 물체와 매칭이 되지 않아도 되는 추상적인 수, 복소수를 이용한 연산 체계도 가능하다는 것이 드러난 것이다. 봄벨리는 고차 방정식의 해법을 연구하는데 복소수가 중요할 것이라고 얘기한다. 그러나 그 후로도 세월이 많이 흐른 이후에야 다시 수학자들은 복소수를 이용한 연산 체계를 고민한다. 그의 업적을 기리기 위해 달 분화구의 이름 중 하나를 Bombelli로 지었다고 한다.
데카르트(1596-1650)는 ‘기하학’에서 "참인 근 혹은 거짓인 근(음수근)이 반드시 실수는 아니다. 때로는 허수 (imaginary number)일 수 있다”라고 했지만 이것을 수로서 인정하지 않는다. 흥미로운 얘기 중 하나는 복소수 적분의 기본 이론, 그리고 복소수를 이용하여 수많은 수열의 수렴성을 연구한 위대한 수학자 Cauchy가 허수가 수임을 부정한 사실이다. 해석학(특히 복소 해석학)을 공부하면서 Cauchy의 이름을 피해 나갈 수는 없다.
1748 오일러는 허수를 i로 표시하고 복소수의 지수에 관한 위대한 업적을 남긴다. 아래 공식에 theta 자리에 pi를 넣으면 수학자들의 투표에서 “수학 역사상 가장 위대한 수학 공식”이라고 불리는 공식이 탄생한다. exp(i x pi)=-1이라는 공식에는 e, i, pi라는 지수/허수/원주율 세 신비로운 수들 간의 관계를 단 하나의 수식으로 보이기에 미학적 아름다움마저 느껴진다. 물론, 문과생들은 복소수를 접할 기회가 없었을 것이기에 별 감흥이 없을 것으로 생각된다.

1799년 노르웨이 건축/수학자 베셀(caspar wessel, 1745-1818)은 아래 그림과 같이 실수를 가로축에 허수를 세로축에 나타내는 복소 평면의 개념을 발표한다. 이것을 프랑스 수학자 아르강이 프랑스어로 번역하면서 “argand diagram”이라고도 부른다.

===================================
중요한 인물은 아니지만 복소수와 관련된 다른 수학자 한명만 더 얘기하자. 오일러의 우아한 공식이, 삼각함수의 중요한 아래 공식을 드 무아브르(De Moivre’s formula, 1667-1754)라는 프랑스 수학자가 발견한다.
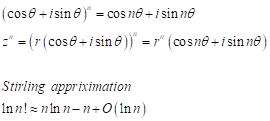
그는 평생을 교수 job을 구하지 못하고 가정교사로 넉넉하지 못하게 살다가 죽는다. 노년에 자신의 수면시간이 매일 15분씩 증가하는 것을 발견하고 정확히 1754/11/27에 죽을 것을 예측하고 실제 그날 사망한다 (철학자나 수학자들 중 약간 psychotic 한 분들이 많은 듯 함, 그 날짜를 맞추려고 일부러 조금씩 더 잤다는 ^^). 증명은 sine/cosine 법칙과 귀납법을 사용하면 간단하다. 드 무아브르는 또한 오늘날 우리가 Stirling 공식이라고 알고 있는 factorial의 근사 공식을 최초로 만든 사람이기도 하다. Stirling 공식은 공학/물리학에 있어 아주 중요한 근사식 중 하나이다.
==================================
마지막으로 복소수를 이용한 아름다운 그림들을 몇 점 감상해 보자. Fractal theory에 나오는 그래프이고, 학부생들이 컴퓨터 그래픽을 배우면 항상 그려보면서 자아도취에 빠지기도 하는 그림이다. 부분을 확대하면 전체가 다시 나타난다. Self similarity 혹은 scale invariant 특성을 가진다고 얘기한다. 아래의 수열을 계산해서 좌표값들을 display 하면 나오는 패턴들이다.
위에서부터 각각




'수학사' 카테고리의 다른 글
| 리만 가설 (0) | 2021.01.29 |
|---|---|
| 조화급수와 리만제타 함수 (0) | 2021.01.28 |
| 알콰리즈미, 알고리듬이라는 이름의 아랍 수학자 (0) | 2021.01.27 |
| 페르마와 데오판토스 (0) | 2021.01.27 |
| 작도와 대수학 (0) | 2021.01.26 |




