우주의 곡률

 

#천문학

 

오늘은 잠깐 양자역학에서 벗어나서 우주 규모의 얘기를 해 보자. 상대성님께서 우주의 나이를 계산하는 식을 올렸기에 잠시 배경 지식을 설명해 보자. 그러나, 수식이 많기에 이해가 쉽지는 않다. 이번에는 우주론의 시작, 우주의 거리를 정의하기 위한 FRW metric을 얘기해 보자. 1930년대 중반에 나온 이론으로 우주의 팽창을 고려한 우주 단위의 metric이다. 상대성님의 자료 이해에, 우주의 나이를 계산하는 수식의 이해에 도움이 될 것이다 (덜 엄밀하지만 그냥 1/H로 우주의 나이를 구할 수도 있다 ^^).

 

우주 스케일에서 metric은 크게 보면 두가지를 얘기한다. 하나는 우주 전체의 dynamics를 표시하는 질량이 존재하는 공간까지 포함하는 FRW metric이고, 하나는 질량이 존재하지 않는 곳에서의 아인슈타인 중력장 방정식의 해인 Schwartzshild metric이다. 전자는 우주의 팽창을 설명하는 Friedmann equation으로 연결되고, 후자의 경우 blackhole dynamics를 묘사한다.

 

아래 수식전개에서 공간의 곡률에 대해서 얘기한다. 곡률은 곡선에 접원을 그렸을 때, 그 원의 반경의 역수로 정의되기도 하고, Ricci scalar로 정의하기도 한다. 우주의 공간에 원을 그렸을 때, 평면에서 그린것 대비 면적이 얼마나 큰지, 즉, 우주 공간이 얼마나 휘어있는지를 나타낸다. 흔히 직관적으로 생각하면 원통의 표면은 곡률이 존재할 것 같지만, 계산해보면 곡률은 0인 flat space이다. 

 

1.Flat Euclidean space

일반적인 편평한 3차원 시공간의 두 지점 사이의 길이는 우리가 흔히 아는데로 아래와 같이 정의된다. 피타고라스 정리에 의해서이다. 세 축의 길이의 제곱으로 계산된다.

 

회전 변환을 해도 두 지점의 길이, 한 벡터의 길이, 각도 등은 변하지 않는다. 즉 회전변환을 나타내는 행렬이 R이라고 하면, R은 orthogonal matrix이고, R^TR=I임을 이용하면 아래와 같다.

 

2.Positively curved space

이제 곡률이 양수인 공간, 예를 들면 3차원 유클리드 공간의 구의 표면에 해당하는 2차원 공간 S2에서의 길이를 생각해 보자. 위의 좌측 그림에서 두번째 경우이다.

 

이것을, 머리속으로 그릴 수는 없지만, 4차원 유클리드 공간의 3차원 구에 해당하는 공간에서의 길이로 확장할 수 있다 (물론 n 차원까지 확장이 가능하다). 즉,

 

3.negatively curved space

이제 곡률이 음수인 공간, Hyperboloid 공간을 생각하자. 4차원 Lorentzian space R(1,3)의 표면에 해당하는 쌍곡선 공간을 H3공간이라고 부른다. 그 공간에서 두 지점의 길이는 제일 마지막 좌표의 부호를 -1로 바꾼 것에 해당하고 (유클리드 공간과 차이가 있음), 앞서의 과정으로 두 지점의 길이를 구하는 과정을 보면,

 

위의 세가지 경우를 모두 정리하면 아래와 같은 단일한 표현이 가능하다. 아래에서 (x,y,z,w)에 전체적으로 a를 곱할수 있다. 우주의 팽창을 설명하기 위해서이다. 그러면 Cartesian 공간에서 아래와 같이 두 지점의 길이를 구할 수 있는 단일한 형태의 표현을 얻는다.

 

FRW metric을 유도하기 위해서는 위의 metric을 polar coordinate 즉 (r,theta, phi)좌표로 변형해야 한다. 구형 좌표계로 변경하는 이유는 대칭성을 이용할 수 있기 때문이다.

 

FRW metric 은 우주가 시간에 따라 팽창함을 묘사한다. 시간이 흐름에 따라, 우주 공간에서 1미터라고 부르는 자가 점점 부풀어 오르는 것이다. 물질들이 폭발하듯이 팽창하는 것이 아니라, 물질들은 그대로 있는데, metric이 팽창하는 경우이다. 이러한 팽창 계수를 앞서 본 수식에서 a가 나타내고 이것이 시간에 따라 달라지기에 a(t)로 표시된다. 이제, 상대성 이론에서 자주 접한 4차원 시공간의 두 지점 사이의 거리, 두 이벤트 사이의 거리를 나타내 보자.

 

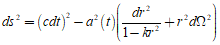
Robertson과 Walker 가 1930년대 중반에 독립적으로 발견한 homogeneous (균일), isotropic (등방), expanding (팽창) 우주를 기술하는 metric이다.

 

이러한 metric 공간에 아인슈타인의 장방정식을 적용하거나, Newton의 고전적인 방법을 사용하면 다음 포스팅에서 소개할 우주 단위의 존재의 움직임을 나타내는 방정식인 Friedmann equation을 유도할 수 있다.