자신을 인식하는 물질, 존재와 의식... 자연철학적 접근
사영공간 본문
아핀 평면(Affine plane)은 점과 선으로 구성되고 두 점으로 유일한 직선이 지정되고, 직선은 최소 2개의 점을 가지고, 직선위에 있지 않은 한점을 지나면서 그 직선을 지나지 않는 유일한 직선이 지정되고(Playfair’s axiom), 한 직선위에 있지 않은 세 점을 지정할 수 있다는 공리들이 성립하는 공간이다. 바로 유클리드 공간이 대표적인 아핀 공간이다.
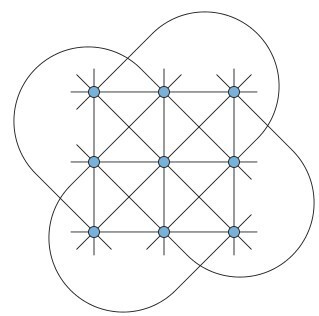
이 개념을 유한체 기하학에 응용하면 유한체 유클리드 공간의 개념을 확장한 아핀 공간을 정의할 수 있다. 유한체 기하학에서 직선은 유한개의 점들로 구성되며 2개의 직선은 한점에서 만나며 평행한 두 직선이 존재한다. 또한 한 직선에 있지 않은 점을 지나며 그 직선과 평행한 직선이 유일하게 존재한다(playfair’s axiom). 어떤 세개도 한 직선위에 있지 않은 4개의 점이 존재한다는 공리를 만족시킨다. 아래는 아래는 9개의 점과 12개의 직선으로 구성된 3차의 (한 직선위에 3개의 점들이 존재) 아핀 공간이다.
이 개념을 유한체 기하학에 응용하면 유한체 유클리드 공간의 개념을 확장한 아핀 공간을 정의할 수 있다. 유한체 기하학에서 직선은 유한개의 점들로 구성되며 2개의 직선은 한점에서 만나며 평행한 두 직선이 존재한다. 또한 한 직선에 있지 않은 점을 지나며 그 직선과 평행한 직선이 유일하게 존재한다(playfair’s axiom). 어떤 세개도 한 직선위에 있지 않은 4개의 점이 존재한다는 공리를 만족시킨다. 아래는 아래는 9개의 점과 12개의 직선으로 구성된 3차의 (한 직선위에 3개의 점들이 존재) 아핀 공간이다.
2. 곡선의 분류: 사영 공간
곡선의 성질을 연구하고 싶다. 그러나, 곡선의 종류는 너무 많다. 예를 들어 직선의 방정식을 보자. f(x,y)=ax+by+c=0 을 만족시키는 어떠한 것들도 직선을 표현한다. 그러나, 우리는 직선을 모두 표현하고 싶은 것이 아니라, 직선이라는 것의, 그 본질적인 것의 성질에 관심이 있다. 그러면 예를 들어 x+y-1=0과 x+y=0의 차이는 있을까? 없을 것이다. 둘다, 기울기가 -1인 직선일 뿐이다. 직선이 어디에 있느냐가 본질적인 질문이 아니라면, 우리는 일단, 모든 직선이 원점을 지난다고 가정할 수 있다.
그러면 f(x,y)=ax+by 로 변수 하나가 줄어든다. 이제, 다시 생각해 보자. y=x 와 2y=2x는 다른 직선인가? 분명히 (a,b)=(1,1) 과 (2,2)이니 달라보이지만 그 둘은 본질적으로 같은 직선이다. 즉, (x,y)와 (kx,ky)는 모두 같은 직선이라고 생각한다 (equivalence relation). 2차원 공간에서 원점을 지나는 모든 직선은 y=1이라는 직선 혹은 {(x,1),x는 실수} 와 오직 한점에서 만난다. 즉, (x,y)~(x/y,1) 이라면 본질적으로 (x,y=1)위의 한 점이 하나의 직선들에 1:1 mapping 된다. 단, x축은 y=1과 만나지 않는데, 이것은 무한대에서 만난다고 가정하기에 사영 공간에는 무한대라는 점이 포함되어 있다. 무한대는 x축을 나타낸다. 이것을 다르게 표현하면 x^2+y^1=1 이라는 원을 그리고, 그 위의 원점 대칭인 두 점이 같은 직선을 가르킨다는 가정을 하면, 원위의 한 점이 직선 하나에 대응한다.
곡선의 성질을 연구하고 싶다. 그러나, 곡선의 종류는 너무 많다. 예를 들어 직선의 방정식을 보자. f(x,y)=ax+by+c=0 을 만족시키는 어떠한 것들도 직선을 표현한다. 그러나, 우리는 직선을 모두 표현하고 싶은 것이 아니라, 직선이라는 것의, 그 본질적인 것의 성질에 관심이 있다. 그러면 예를 들어 x+y-1=0과 x+y=0의 차이는 있을까? 없을 것이다. 둘다, 기울기가 -1인 직선일 뿐이다. 직선이 어디에 있느냐가 본질적인 질문이 아니라면, 우리는 일단, 모든 직선이 원점을 지난다고 가정할 수 있다.
그러면 f(x,y)=ax+by 로 변수 하나가 줄어든다. 이제, 다시 생각해 보자. y=x 와 2y=2x는 다른 직선인가? 분명히 (a,b)=(1,1) 과 (2,2)이니 달라보이지만 그 둘은 본질적으로 같은 직선이다. 즉, (x,y)와 (kx,ky)는 모두 같은 직선이라고 생각한다 (equivalence relation). 2차원 공간에서 원점을 지나는 모든 직선은 y=1이라는 직선 혹은 {(x,1),x는 실수} 와 오직 한점에서 만난다. 즉, (x,y)~(x/y,1) 이라면 본질적으로 (x,y=1)위의 한 점이 하나의 직선들에 1:1 mapping 된다. 단, x축은 y=1과 만나지 않는데, 이것은 무한대에서 만난다고 가정하기에 사영 공간에는 무한대라는 점이 포함되어 있다. 무한대는 x축을 나타낸다. 이것을 다르게 표현하면 x^2+y^1=1 이라는 원을 그리고, 그 위의 원점 대칭인 두 점이 같은 직선을 가르킨다는 가정을 하면, 원위의 한 점이 직선 하나에 대응한다.
=========================
어떤 2변수 2차 함수 g(x,y)=(a)(x^2)+2(b)(xy)+2(c)(x)+(d)(y^2)+2(e)(y)+f=0 이라는 곡선을 생각해 보자. 이것은 아래와 같이 행렬 표현을 할 수 있다. 아래에서 z라는 변수를 추가한 이유는, 2차함수를 사영공간에 배치시키기 위해서이다. 즉, (x,y,z)와 (kx,ky,kz)는 모두 동일한 직선상의 점으로 인식시키기 위함이다. Z를 추가함으로써 각 항들이 모두 2차항이 되어 scaling이 자연스럽게 이루어짐을 알 수 있을 것이다. 즉, (x,y,z)~(kx,ky,kz)의 관계에 있다.
어떤 2변수 2차 함수 g(x,y)=(a)(x^2)+2(b)(xy)+2(c)(x)+(d)(y^2)+2(e)(y)+f=0 이라는 곡선을 생각해 보자. 이것은 아래와 같이 행렬 표현을 할 수 있다. 아래에서 z라는 변수를 추가한 이유는, 2차함수를 사영공간에 배치시키기 위해서이다. 즉, (x,y,z)와 (kx,ky,kz)는 모두 동일한 직선상의 점으로 인식시키기 위함이다. Z를 추가함으로써 각 항들이 모두 2차항이 되어 scaling이 자연스럽게 이루어짐을 알 수 있을 것이다. 즉, (x,y,z)~(kx,ky,kz)의 관계에 있다.
위에서 Q는 대칭 행렬이므로 항상 대각화가 가능하고, 따라서, 변수들끼리 서로 섞이는 경우를 선형 변환을 통해서 제거할 수 있다. 제거 후 각 항에 곱해지는 것은 Q행렬의 고유치(eigen value)들인데, 그것들은 변수 치환을 통해서 normalize 가능하므로 2차함수들은 본질적으로 다음과 같은 5가지 형태만이 존재한다.
결론은, 2차함수는 다양한 표현이 가능하지만, 본질적으로 unit circle와 간단한 변환 관계에 있는 도형들 외에는 없다. 따라서 2차 함수에 대해서는 원의 성질만 정확하게 이해하면 다른 도형들의 성질은 파생적으로 알 수 있다.
====================
3. 타원 곡선: Weierstrass form
타원을 표현하는 다양한 방법이 있지만, 앞에서 보았듯이, 변수들간의 선형적인 변환에 의해서 비교적 간단한 본질적인 형태로 나타낼 수 있다. 그 형태가 Weierstrass form이다.
3.1. Nonsingular, Nondegenerate Curves
타원 곡선에 특이점이 존재한다는 얘기 즉, f(x,y)=0 가 (x,y)에서 singular 하다는 얘기는 그 점에서 곡선의 접선(tangent line)이 정의될 수 없는 경우를 의미한다. 그 경우는 아래와 같은 세가지 경우가 존재한다. 각각 cusp, intersection, isolated point들이 존재하는 경우들이며 각 곡선의 예는, y^2=x^3, x^3+x^2, x(x+1)^2 인 경우들이며, 모두 gradient=0인 경우에 발생한다. 중근이 존재하는 경우들이다.
====================
3. 타원 곡선: Weierstrass form
타원을 표현하는 다양한 방법이 있지만, 앞에서 보았듯이, 변수들간의 선형적인 변환에 의해서 비교적 간단한 본질적인 형태로 나타낼 수 있다. 그 형태가 Weierstrass form이다.
3.1. Nonsingular, Nondegenerate Curves
타원 곡선에 특이점이 존재한다는 얘기 즉, f(x,y)=0 가 (x,y)에서 singular 하다는 얘기는 그 점에서 곡선의 접선(tangent line)이 정의될 수 없는 경우를 의미한다. 그 경우는 아래와 같은 세가지 경우가 존재한다. 각각 cusp, intersection, isolated point들이 존재하는 경우들이며 각 곡선의 예는, y^2=x^3, x^3+x^2, x(x+1)^2 인 경우들이며, 모두 gradient=0인 경우에 발생한다. 중근이 존재하는 경우들이다.
타원곡선 f(x,y)이 f(x,y)=g(x,y)h(x,y)와 같이 인수분해가 되는 꼴이면 이 경우 f(x,y)가 degenerate(축퇴)되었다고 얘기한다. 그렇지 않은 경우 non-generate하다고 얘기한다. 예를 들면 x^2-y^2=0은 (x-y)(x+y)로 인수분해되므로 degnerate된 형태이다.
3.2. If f(x,y) is nondegenerate, nonsingular cubic polynomial, then f(x,y)=0 can be represented by y^2=x^3+ax+b where discriminant 4a^3+27b^2 is not zero.
증명: 간단한 경우만.. 일반적인 경우는 복잡하니, 아래에서 만약 characteristic of K가 2 혹은 3이 아닌 경우만 살펴본다. Characteristic=n이란 K의 1을 n번 더하면 0이되는 수를 말한다. 예를 들어 로 나눈 나머지들로 구성된 그룹 z_5의 경우, 1+1+1+1+1=0 (mod 5) 이므로 char(z_5)=5이다. R혹은 C의 경우 char(R or C)=infinity이다.
3.2. If f(x,y) is nondegenerate, nonsingular cubic polynomial, then f(x,y)=0 can be represented by y^2=x^3+ax+b where discriminant 4a^3+27b^2 is not zero.
증명: 간단한 경우만.. 일반적인 경우는 복잡하니, 아래에서 만약 characteristic of K가 2 혹은 3이 아닌 경우만 살펴본다. Characteristic=n이란 K의 1을 n번 더하면 0이되는 수를 말한다. 예를 들어 로 나눈 나머지들로 구성된 그룹 z_5의 경우, 1+1+1+1+1=0 (mod 5) 이므로 char(z_5)=5이다. R혹은 C의 경우 char(R or C)=infinity이다.
위의 여러 논의들의 결과는 타원곡선에 관한 이해를 위해서 모든 Elliptic curve를 모두 조사할 필요가 없이, Weierstrass form의 Elliptic curve만 조사하면 된다는 것 즉, y^2=x^3+ax+b 형태만 연구하면 된다.
이러한 타원 곡선의 종류도 무지무지 많고 동일한 타원 곡선의 경우에도 그 표현이 다양하게 주어질 것이다. 타원 곡선 상의 다양한 표현은 그들 사이의 변환 관계인, Isogeny에 의해서 표현될 수 있기에 Isogeny, dual-isogeny, isomorphism, j-invariance 등 에 대한 이해가 필요하다. Iso-geny에 대한 이해와 그 용어에 대한 설명에 충분히 익숙해지면, 유한체 상의 타원곡선의 해의 개수의 경계를 설명하는 하세 베유 정리는 짧게는 3~4줄, 길게는 20줄 이내에 증명이 가능하다.
이러한 타원 곡선의 종류도 무지무지 많고 동일한 타원 곡선의 경우에도 그 표현이 다양하게 주어질 것이다. 타원 곡선 상의 다양한 표현은 그들 사이의 변환 관계인, Isogeny에 의해서 표현될 수 있기에 Isogeny, dual-isogeny, isomorphism, j-invariance 등 에 대한 이해가 필요하다. Iso-geny에 대한 이해와 그 용어에 대한 설명에 충분히 익숙해지면, 유한체 상의 타원곡선의 해의 개수의 경계를 설명하는 하세 베유 정리는 짧게는 3~4줄, 길게는 20줄 이내에 증명이 가능하다.
반응형
'수학이론' 카테고리의 다른 글
| 호몰로지 (0) | 2022.07.30 |
|---|---|
| 군이론 (0) | 2022.07.30 |
| 소수 판별 (0) | 2022.07.30 |
| 타원 곡선 암호(ECC) (0) | 2022.07.30 |
| Birch and Swinerton-Dyer 문제 (0) | 2022.07.30 |
Comments