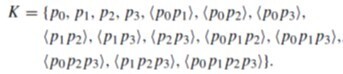호몰로지

Euler characteristic은 도형의 꼭지점, 모서리 면 사이의 관계식으로 x=V-E+F 이며, convex polyhedron의 경우 (흔히 말하는 n면체) V-E+F=2라는 오일러 polyhedron 공식(1758)을 얻는다. 이전에 얘기한데로 이것은 3차원상의 2차원 구면 S2의 오일러 지표에 해당한다. Convex란 그 집합의 서로 다른 두 점을 연결한 선의 모든 점들이 그 집합에 속하는 경우를 의미하는데, 도형을 이상하게 만들어서, convex 하지 않다면 위의 공식은 성립하지 않는다.

아래는 tetrahemilhexaqhedron이라는 도형은 직관적으로 이해하기가 쉽지는 않지만, 이것을 펼쳐서 해석하면, 4개의 삼각형과 3개의 사각형의 조합으로 이루어지며, F=7, E=12, V=6 이 되어, 오일러 표수가 1인 도형이다. 이 외에 다양한 도형에 대해서 Euler characteristic은 2가 아니다. Convex하지 않기 때문이다.

Video Player

 

• 

도형의 표면을 분석하면 이렇게, 2차원 Face, 그리고 그들이 boundary인 1차원 edge, 그리고 그들의 경계인 0차원 점으로 분해가 가능하며, 반대로, 점들을 조합하여 선을, 선들을 조합하여 면을, 면들을 조합하여 3차원 표면을… 이렇게 계속 확장이 가능하다고 유추할 수 있으며, 이 과정을 통해서 우리는 비록 그림으로는 그릴 수 없지만, 추상적인 공간에 존재하는 도형을 수학적으로 만들 수 있다. 그러면, 이렇게 만든 n 차원 공간의 도형에서도 여전히 Euler characteristic은 의미가 있을 것이며, 그것은 3차원 공간에서 생각하는 그것들과 동일할 것인가라는 질문이 나올 수 있다.

0차원 점들(C0) -> 1차원 선들(C1) -> 2차원 면들(C2) -> 3차원 부피들(C3) -> … 이렇게 진행하다보면 복잡한 도형이 탄생한다. 이러한 연결을 CW-complex (closure-finite weak topology complex)라고 부른다. 우리가 말하는 3차원 도형들은 2차원 CW complex 들이다. 특히, 모든 면들을 삼각형으로 쪼개어 표현할 수 있다면 이것을 simplicial complex라고 부른다. 이제 n 차원 공간의 도형의 오일러 지표는 2차원의 경우를 다음과 같이 확장할 수 있다.

X=k0-k1+k2-k3+…

위에서 kn은 n-simplex (n차원 simplex, 0차원=점, 1차원=선, 2차원=삼각형,3차원=tetrahedron…)의 개수를 말한다. C2의 경우 k0=V, k1=E, k2=F 로 k0-k1+k2=V-E+F로 흔히 알고 있는 오일러지표이다.

이것을 CW가 아닌 일반적인 위상 공간(topological space)로 확장하면 오일러 지표는 다음과 같이 betti number로 표현된다. n번째 베티 수인 bn은 은 n번째 singular homology group Hn의 rank (rank는 generator의 수)에 해당한다. bn은 간단히는 n차원 구멍의 수를 의미한다. 이것은 점, 선, 면으로 이루어진 도형에서 그들의 개수로부터 정의되는 앞서의 정의들과는 상이하지만, 아래와 같은 정의로 구한 오일러 지표와 앞서의 정의로부터 구한 지표들이 일치함이 수학적으로 증명되어 있다.

X=b0-b1+b2-b3+…

=====================

G1과 G2가 Abelina group이라고 할 때, f:G1->G2 가 f(x+y)=f(x)+f(y) 이면 이것을 homomorphism이라고 한다. f:Z->Z2={0,1}, f(2n)=0, f(2n+1)=1 이 그 예이다. Ker(f)=0이면 monomorphism 혹은 injective라고 얘기하고, im(f)=G2이면 epimorphism 혹은 surjective 이다. 앞서의 예는 epimorphism이며 monomorphism은 아니다.

Normal subgroup H⊂G에 대해서 G/H는 qoutient group을 이루고, x-y∈H일 때, x~y 로 그 둘은 같은 equivalence class에 속한다. 즉, 그 둘을 같은 것을 취급하겠다는 것이다. 이제 Fundamental theorem of homomorphism은 f:G1→G2에 대해서 G1/ker(f)=im(f)이다. 앞서의 예제에서 ker(f)=2Z 이므로 Z/2Z=Z2인 것을 알 수 있다. 일반적으로 Z/nZ= Zn=({0,1,…,n-1},(x+y) mod n) 이다.

G가 abelian group, 즉, +에 대해서 교환법칙이 성립하는 군의 경우라면, 그 군의 구조는 쉽게 파악할 수 있는데, 그것을 말하는 이론이 fundamental theorem of finitely generated Abelian group이며 그 내용은 모든 가환 그룹의 형태는 아래와 같이 rank r의 infinite order cyclic group r개와 rank k1~kp의 나머지 cyclic group으로, 즉 cyclic group의 direct sum으로 나타낼 수 있다는 것이다.

• 

========================

도형은 아래 그림과 같은 simplex로 구성된다. 아래 그림은 0~3까지의 simplex (점,선, 면, 입체)를 보여준다. 이것을 n차원으로 확장하면, 추상적인 공간의 도형을 만들 수 있다. <p0> 은 고립된 점들의 집합을, <p0p1>은 선을 <p0p1p2>는 triangle을, <p0p1...pr>은 r-simplex를 표현한다. 수학적으로 r-simplex s(r)은 다음과 같이 정의된다.

• 

• 

r-simplex에서 0<=q<=r 일때, q+1개의 점을 선택하면 면/선/점이 선택된다. 예를 들면 <p0p1p2p3>의 삼각뿔에서 3개의 점을 선택하면, 예를들면 <p0p1p2>, 해당 면이 결정되고, 2개의 점을 선택하면, <p0p1>은 해당 선을 결정한다. q+1개로 결정되는 면(혹은 선,점)을 q-face라고 부른다. <p0p1p2p3>는 자기 자신이 되어 face가 되는데, 자기자신을 제외한 face를 proper face라고 부른다.

simplex들은 도형을 구성할 수 있는 재료들이다. 이것들을 잘 조합하면 도형을 만들 수 있다. 여기서 잘 조합한다는 말의 수학적 정의는

• 

이며, 아래 왼쪽 그림은 가능하지만, 오른쪽 그림은, 두 edge의 만나는 점에 해당하는 점이 그 집합에 해당하지 않으므로 잘 결합되었다는 조건에 위배되고 따라서 simplicial complex가 아니다.

• 

<p0p1p2p3>를 표현하는 simplex complex는 아래와 같다. 모든, 꼭지점, 모서리, 면, 그리고 자기 자신을 포함한다. 즉, simplical complex는 그 원소로 simplex들을 가진다. 만약 simplex가 R^m 유클리드 공간에 존재한다면 그러한 K를 K polyhedron 이라고 부른다. K의 dimension 은, 내부에 포함하는 simplex 중 가장 큰 dimension으로 정의되고, dim (r-simplex)=4 이다. 즉, <p0p1p2p3> tetrahedron의 차원은 3, 즉 3차원 도형이다. 바로 위에 hqdlsms (a)도형의 경우, 점들의 수는 많지만, 가장 차원이 높은 면(q-face)가 2차원이므로 dim(K)=2가 될 것이다.

• 

구부러진 도형의 경우, homeomorphism에 의해서 simplical complex K에 mapping 시킬 수 있다면, 즉 f: K->X 라면, X는 triangulable하다고 얘기하고, (K,f)를 triangularion of K라고 얘기한다. 예를 들면, 원의 경우, hemomorphism에 의해서 tetrahedron으로 변형할 수 있으므로, 원에 대한 연구는 사면체를, 반대로 사면체에 대한 연구는 원에 대한 성질들을 연구함으로써 분석할 수 있다.

이제, q-face의 앞뒤면을 구별하기 위하여 q-face의 방향을 정의할 수 있다. 어떤 방향을 잡던 일관되게 잡으면 될 것이다. 중요한 것은 점들의 순서가 변하면 그 방향성이 변한다는 것이다. 예를 들어 아래 1, 2 simplex의 경우, (p0p1)=-(p1p0)이고, (p0p1p2)=(p2p0p1)=(p1p2p0)=-(p0p2p1)=-(p2p1p0)=-(p1p0p2) 로, 점들의 순서에 따라 면의 방향이 달라진다는 것이다. 일반적으로 (pipjpk)=sgn(P)(p0p1p2) 이며, P는 permutation matrix 이며, sgn(P)는 홀수번 치환은 -1, 짝수번 치환은 1을 의미한다.

• 

Homology를 얘기하기 위하여 먼저 simplex들로 구성된 chain group을 만든다. r-chain group C_r(K)의 정의는 아래와 같다.

• 

이제 boundary operator ∂:r-simplex→(r-1)-simplex 를 도입한다. 먼저 ∂(0-simplex or point)=0 이다. 점에는 경계가 없다. ∂(p0p1)=p1-p0 로 정의된다. p0, p1, p2로 이루어진 삼각형을 생각해 보면, 세 모서리 p0p1, p1p2, p2p0는 cycle을 형성한다. cycle을 이룬다는 얘기는 그 공간에 2차원의 구멍(삼각형 모양 구멍)이 있다는 얘기이므로 ∂(p0p1)+ ∂(p1p2)+ ∂(p2p0)=p1-p0+p2-p1+p0-p2=0 이 되게 정의가 된 것이다. 즉, 어떤 공간에 속이 빈 cycle을 이루는 모서리들의 집합이 있다면, 즉 구멍이 있다면 boundary operation의 결과 0에 mapping된다.

이제 다음과 같이 차원이 줄어드는 chain group의 연쇄적인 연결로 구성된 chain complex C(K)를 생각해 보자. 만약 ∂_r(c)=0 일때, c를 r-cycle 이라고 부르며 이것들의 집합, Z_r(K)=ker(∂_r)를 r-cycle group이라고 부른다. 그리고, c=∂_(r+1) (d) 를 r-boundary라고 부르며, 이것들의 집합 B_r(K)=im(∂_(r+1))를 r-bondary group이라고 부른다.

• 

Chain complex의 가장 큰 특징 중 하나는 다음 수식으로 대변된다. 예를 들면 4각형의 boundary를 자르면 모서리들이 나오는데, 그 모서리들은 cycle을 이루므로 다시 boundary map을 적용하면 0이 된다는 사실이다. 아래에서 만약 im()=ker()이면, C(K)를 exact sequence라고 부르며, 얼마나 exact하지 않은지는 homology group 으로 표현된다.

• 

내부가 채워진 도형은 공간에 hole을 만들지 않는다. 그러나 그 도형의 경계, boundary와 원래 구멍으로서의 원의 가장자리는 동일하다. 내부가 채워진 원, 2차원 공간의 disk를 D2라고 부르고, D2의 경계인 1차원의 원 S1을 생각해 보자, ∂(D2)= S1 이고, ∂∂ (D2)= ∂(S1)=0이다. 즉, ∂에 의해서 만들어진 boundary에 다시 ∂를 하면, 즉 경계 연산자 ∂를 두번 적용하면 항상 0이 되게 되어 있지만, 그들이 모두 구멍을 의미하지는 않는다. H_r=ker(∂_r)/im(∂_(r+1)) 로 내부가 채워진 경계로서의 cycle이 아니라, 내부가 비어있는 4차원 hole의 개수를 표현한다.

==================

실제로 homology group을 계산하는 것은 아주 간단한 도형의 경우라도 길고 지저분한 계산 과정을 거쳐야 하므로, 그냥 타인의 계산을 믿고 테이블을 참조하는 것이 마음 편하다. 아래에 여러가지 도형에 대해서 homology group을 정리한 것을 옮겨본다.

• 

• 

우리가 알고 있는 n-면체들은 모두 2-sphere와 homeomorphic 하니 그들의 H0=Z이고 H2=Z이고 나머지는 모두 0이다. H0가 의미하는 것은 그 도형에서 연결된 집합의 개수이고, H2는 2차원 구멍의 개수이다. 구의 표면을 의미하는 2-shpere S2의 경우, 모든 점들이 연결되어 있다는 것을 H0=Z로 알 수 있다. 만약 H0=ZxZ라면 2개의 분리된 집합들의 합집합으로 표현되는 도형일 것이다. 그리고, H2=Z라는 것은 2차원 구멍(내부의 3차원을 파낸)의 개수가 하나라는 것을 의미한다.

앞서 Betti number b_n은 H_n의 rank이고 rank란 H_n=ZxZx..xZ의 Z의 개수에 해당하므로 2sphere의 Betty number는 b0=1, b1=0, b2=1 에 해당하며 2-sphere의 Euler 지표는 X=b0-b1+b2=2에 의해서 V-E+F=2라는 오일러 공식이 나온다.

위에서 Torus의 경우를 보면 T=S1 x S1으로 표현할 수 있다. Torrus는 모든 점들이 하나로 연결되니 H0=Z이고, 1차원 hole은 큰원, 작은원 방향으로 2개이니 H1=ZxZ이고, 내부에 도너츠의 내부를 들어낸 구멍이 존재하니 H2=Z로 표현된다.
Torus 의 경우 Euler 지표 X=b0-b1+b2=1-2+1=0 이다.

• 

만약 아래 그림과 같이 구멍이g개인(genus=g)도너츠의 표면에 해당하는 공의homology를 구하면 H1=ZxZx...Z 의 rank g의 cyclic group으로 표현될 것이다. genus g인(즉, 손잡이가 g개인) torus의 Euler 지표 X는 2-2g 로 주어진다. 구의 표면의 경우 손잡이가 없으므로 X=2 이기에 다시 오일러 공식을 확인할 수 있다.

•