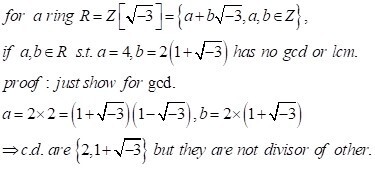자신을 인식하는 물질, 존재와 의식... 자연철학적 접근
환이론 2 본문
현대대수학의 ring구조에 대한 두번째 글이다. 내용은 많이 복잡하니, 현대 대수에 관심이 없다면 전혀 읽을 필요가 없다.
============================
9. Euclidean domains
정수 환 Z의 모든 ideal은 principle ideal이다. (증명: I 가 Z의 ideal이라면, 그 중 가장 크기가 작은 원소 b∈I 가 존재할 것이다. Ideal의 정의상 bZ⊂I 이다. a∈I인 원소 하나를 고르면, 정수이기에 a=bq+r (r=0~b-1) 로 r<b인 r을 찾을 수 있을 것이다. 그러면 r-a=qb∈bZ⊂I 이니 r=I+I∈I 가 되어 b가 가장 작은 원소라는 가정에 위배된다.)
이것을 정수가 아닌 일반적인 Ideal에 대해서도 얘기할 수 있을 것인가? 위의 증명 과정을 보면, 증명의 핵심은 a=qb+r 연산이 가능하다는 것에 있다. 모든 Ideal에 대해서 이것이 가능할 것인가? 그렇지 않을 것이기에 다음과 같이 Euclidean domain을 정의한다. 즉, 추상적인 대수를 자연수처럼 여길 수 있는 norm 을 그 공간에 도입할 수 있는 integral domain을 Euclidean domain이라고 부른다.
============================
9. Euclidean domains
정수 환 Z의 모든 ideal은 principle ideal이다. (증명: I 가 Z의 ideal이라면, 그 중 가장 크기가 작은 원소 b∈I 가 존재할 것이다. Ideal의 정의상 bZ⊂I 이다. a∈I인 원소 하나를 고르면, 정수이기에 a=bq+r (r=0~b-1) 로 r<b인 r을 찾을 수 있을 것이다. 그러면 r-a=qb∈bZ⊂I 이니 r=I+I∈I 가 되어 b가 가장 작은 원소라는 가정에 위배된다.)
이것을 정수가 아닌 일반적인 Ideal에 대해서도 얘기할 수 있을 것인가? 위의 증명 과정을 보면, 증명의 핵심은 a=qb+r 연산이 가능하다는 것에 있다. 모든 Ideal에 대해서 이것이 가능할 것인가? 그렇지 않을 것이기에 다음과 같이 Euclidean domain을 정의한다. 즉, 추상적인 대수를 자연수처럼 여길 수 있는 norm 을 그 공간에 도입할 수 있는 integral domain을 Euclidean domain이라고 부른다.
당연히(field에서 모든 원소의 역원이 존재하기에), 모든 field는 E.D. 이다. 정수환인 Z with N(n)=n 도 마찬가지이다. 다른 몇가지 예들을 들어보면,
1. Gaussian integer Z[i]=a+bi with N(a+bi)=a^2+b^2
2. Eisenstein integer Z[ω] with f(a+bω)=a^2-ab+b^2.
3. Polynomial ring over a field K, K[x] with f(P)=deg(P) for P∈K[x]
ED 이면 PID(principle ideal domain) 이다. 증명은 Z의 모든 ideal이 PID라는 과정과 동일한데, a=qb+r에서 N(a)=N(q)N(b)+N(r)로 대체만 하면 된다. 따라서 PID가 아니면 당연히 ED가 아니다. 예를 들면 2변수 이상의 모든 polynomial ring over a field K[x,y] 들 혹은 Z[√(-5) 등이 그러하다.
그러면 반대로PID이면 ED이냐? 그렇지 않다. 그러나, 그 예를 찾기는 쉽지 않은데, 거의 모든 교과서에 예로 등장하는 것이 Q(√(-19)라는 특이한 모양의 integer ring이다. 자세한 설명은 생략한다. 또한 A=R[x,y]/(x^2+y^2+1) 이라는 quotient ring도 PID이지만 ED가 아니라고 wiki에 나타나 있다.
===========================
10. Principle ideal domain (PID), gcd, lcm
Integral domain(ID) R 내의 모든 ideal이 principle이면 R을 PID라고 부른다. 앞에서 얘기한데로, ED를 얘기한 이유는 ED이면 PID이기 때문이다. 반대는 성립하지 않는다. PID를 얘기하는 이유는 바로 추상적인 수에 대해서 약수(divisor), 배수(multiple), 공약(배)수, 최대공약수, 최소공배수를 얘기하기 위함이다. 이를 위해서 추상적인 수, ring에서의 먼저 배수, 약수의 개념을 얘기하자. 다른 정의들은 정수의 경우와 거의 동일하지만, gcd와 lcm의 경우 가장 크다, 작다의 개념이 아니라, gcd d의 경우 다른 공약수가 d를 나눌 수 있다면, lcm m의 경우 다른 공배수가 m의 배수라면 모두 성립된다. 예를 들면 d가 gcd라면 -g도, m이 lcm이라면 -m도 lcm이 될 수 있다.
1. Gaussian integer Z[i]=a+bi with N(a+bi)=a^2+b^2
2. Eisenstein integer Z[ω] with f(a+bω)=a^2-ab+b^2.
3. Polynomial ring over a field K, K[x] with f(P)=deg(P) for P∈K[x]
ED 이면 PID(principle ideal domain) 이다. 증명은 Z의 모든 ideal이 PID라는 과정과 동일한데, a=qb+r에서 N(a)=N(q)N(b)+N(r)로 대체만 하면 된다. 따라서 PID가 아니면 당연히 ED가 아니다. 예를 들면 2변수 이상의 모든 polynomial ring over a field K[x,y] 들 혹은 Z[√(-5) 등이 그러하다.
그러면 반대로PID이면 ED이냐? 그렇지 않다. 그러나, 그 예를 찾기는 쉽지 않은데, 거의 모든 교과서에 예로 등장하는 것이 Q(√(-19)라는 특이한 모양의 integer ring이다. 자세한 설명은 생략한다. 또한 A=R[x,y]/(x^2+y^2+1) 이라는 quotient ring도 PID이지만 ED가 아니라고 wiki에 나타나 있다.
===========================
10. Principle ideal domain (PID), gcd, lcm
Integral domain(ID) R 내의 모든 ideal이 principle이면 R을 PID라고 부른다. 앞에서 얘기한데로, ED를 얘기한 이유는 ED이면 PID이기 때문이다. 반대는 성립하지 않는다. PID를 얘기하는 이유는 바로 추상적인 수에 대해서 약수(divisor), 배수(multiple), 공약(배)수, 최대공약수, 최소공배수를 얘기하기 위함이다. 이를 위해서 추상적인 수, ring에서의 먼저 배수, 약수의 개념을 얘기하자. 다른 정의들은 정수의 경우와 거의 동일하지만, gcd와 lcm의 경우 가장 크다, 작다의 개념이 아니라, gcd d의 경우 다른 공약수가 d를 나눌 수 있다면, lcm m의 경우 다른 공배수가 m의 배수라면 모두 성립된다. 예를 들면 d가 gcd라면 -g도, m이 lcm이라면 -m도 lcm이 될 수 있다.
일반적인 ring의 경우에 항상 gcd와 lcm은 존재하는가? 만약 존재한다면 그것은 유일한가의 질문이 있을 수 있다존재성에 대한 질문은, 불행히도 그 답은 No 이다. 어떤 ring에 약수와 배수의 개념이 존재하더라도 gcd와 lcm이 존재하지 않을 수 있다. 예를 들면,
두번째 유일성 질문에 대한 답도 이미 살펴본데로 No 이다. 그러나, 그들을 unit을 매개로한 equivalence로 묶으면 유일하다고 얘기할 수 있다. a,b ∈ R(commutative ring)에서 어떤 u∈R이 존재하여 b=au일 때 그들은 associate라고 부르며 a~b, 즉 equivalence relation을 이룬다. 정수라면, (+a)~(-a), field라면 모든 원소 a,b에 대해서 a=b(a/b)이고 (a/b)가 unit이므로 a~b 이며, 모든 다항식들의 ring인 F[x]의 경우, P(x) ∈F[x] 와 가장 높은 차수가 1인 monic polynomial 이 associate관계에 있다. Gaussian integer Z[i]의 경우 a∈{b,ib,-ib,-b}이면 a~b이다.
만약 어떤 ring R이 integral domain(ID)이라면 a b 이고 동시에 b a 라면 즉, 서로가 서로의 배수라면 a~b이다. 그 이유는 b=ax=(yb)x 이므로 (1-yx)b=0 이므로 xy=1, 즉 x 혹은 y는 unit이기 때문이다. 어떤 ring이 ID가 아니라면 서로가 서로의 배수이더라도 그 둘은 associate 관계가 아니다. 만약 어떤 ring R이 ID라면, gcd와 lcm은 associate 관계를 하나로 본다면 유일하다. PID이면 ID이므로 당연히 gcd, lcm은 equivalence 관계를 고려하면 유일하다. 즉, 존재한다면 유일하다.
이제 다시 첫번째 질문으로 돌아와서, 일반적인 경우 gcd/lcm이 존재하지 않지만, 만약 PID라면 그들은 존재할 것인가? 행복하게도 답은 Yes이다. 그리고 a,b∈R에서 만약 cR=aR+bR이라면 gcd=c이고, aR∩bR=cR이라면 c가 lcm이다. 개략적인 증명은 아래와 같다.
만약 어떤 ring R이 integral domain(ID)이라면 a b 이고 동시에 b a 라면 즉, 서로가 서로의 배수라면 a~b이다. 그 이유는 b=ax=(yb)x 이므로 (1-yx)b=0 이므로 xy=1, 즉 x 혹은 y는 unit이기 때문이다. 어떤 ring이 ID가 아니라면 서로가 서로의 배수이더라도 그 둘은 associate 관계가 아니다. 만약 어떤 ring R이 ID라면, gcd와 lcm은 associate 관계를 하나로 본다면 유일하다. PID이면 ID이므로 당연히 gcd, lcm은 equivalence 관계를 고려하면 유일하다. 즉, 존재한다면 유일하다.
이제 다시 첫번째 질문으로 돌아와서, 일반적인 경우 gcd/lcm이 존재하지 않지만, 만약 PID라면 그들은 존재할 것인가? 행복하게도 답은 Yes이다. 그리고 a,b∈R에서 만약 cR=aR+bR이라면 gcd=c이고, aR∩bR=cR이라면 c가 lcm이다. 개략적인 증명은 아래와 같다.
=============================
간략히 정리해보면 ab=0이면 둘 중 하나는 0인 integral domain(ID), a=bq+r의 연산을 할 수 있는 Euclidean domain(ED), 모든 ideal이 principal ideal 즉 I=aR인 principle ideal (PID)에 대해서 얘기하였고, 이것의 목적은 추상적인 수 공간을 마치 정수처럼 다루고 싶어서였다. 3개들 간의 관계는 ED ⊂PID ⊂ID 였다. PID 이면 앞서 보았듯이 gcd, lcm이 모두 존재함을 보였고, ID이면서 gcd, lcm이 성립하지 않는 예도 보였다.
그러면, 자연스러운 질문은, PID와 ID 사이의 대수구조는 없을까? 즉, ID이면서 PID는 아닌데, 그럼에도 불구하고 gcd, lcm 을 얘기할 수 있는 공간이 존재하지 않을까.. 혹은 그러한 대수 공간을 만들 수 있지 않을까일 것이다. 물론, 답은 Yes이다. ID와 PID 사이에 GCD 가 존재하는 GCD domain이 존재한다. 또한 UFD (unique factorization domain)이 GCD와 PID사이에 존재하면서 다음 복잡한 ring 구조의 Hierarchy를 마무리한다.
rings ⊃ rings ⊃ commutative rings ⊃ integral domains ⊃ ⊃ GCD domains ⊃ unique factorization domains ⊃ principal ideal domains ⊃ Euclidean domains ⊃ fields ⊃ algebraically closed fields
===================
11. UFD=unique factorization domain, Notherian ring
GCD를 얘기하려면 먼저 어떤 수의 약수를 구해야 한다. 약수를 구한다는 얘기는 Ring의 어떤수를 그보다 더 작은 수의 곱으로 표현한다는 얘기이며, 더 이상 나눌 수 없는 수를 보통은 소수, prime number라고 얘기한다. 이것을 추상적인 대수에 대해서도 적용하기 위해서 irreducible, prime이라는 개념을 아래와 같이 정의한다. (1)은 어떤 수를 더 이상 나눌 수 없다는 의미이고, (2)는 ab를 r이 나누면 a 또는 b를 r이 나눈다는 의미인데, 아래 정의를 따르면 2,3,5.. 도 소수이지만, -2, -3, -5도 정수의 체계에서는 소수이다. 즉, 우리가 흔히 알고 있는 자연수의 소수와는 미묘한 차이가 있다.
간략히 정리해보면 ab=0이면 둘 중 하나는 0인 integral domain(ID), a=bq+r의 연산을 할 수 있는 Euclidean domain(ED), 모든 ideal이 principal ideal 즉 I=aR인 principle ideal (PID)에 대해서 얘기하였고, 이것의 목적은 추상적인 수 공간을 마치 정수처럼 다루고 싶어서였다. 3개들 간의 관계는 ED ⊂PID ⊂ID 였다. PID 이면 앞서 보았듯이 gcd, lcm이 모두 존재함을 보였고, ID이면서 gcd, lcm이 성립하지 않는 예도 보였다.
그러면, 자연스러운 질문은, PID와 ID 사이의 대수구조는 없을까? 즉, ID이면서 PID는 아닌데, 그럼에도 불구하고 gcd, lcm 을 얘기할 수 있는 공간이 존재하지 않을까.. 혹은 그러한 대수 공간을 만들 수 있지 않을까일 것이다. 물론, 답은 Yes이다. ID와 PID 사이에 GCD 가 존재하는 GCD domain이 존재한다. 또한 UFD (unique factorization domain)이 GCD와 PID사이에 존재하면서 다음 복잡한 ring 구조의 Hierarchy를 마무리한다.
rings ⊃ rings ⊃ commutative rings ⊃ integral domains ⊃ ⊃ GCD domains ⊃ unique factorization domains ⊃ principal ideal domains ⊃ Euclidean domains ⊃ fields ⊃ algebraically closed fields
===================
11. UFD=unique factorization domain, Notherian ring
GCD를 얘기하려면 먼저 어떤 수의 약수를 구해야 한다. 약수를 구한다는 얘기는 Ring의 어떤수를 그보다 더 작은 수의 곱으로 표현한다는 얘기이며, 더 이상 나눌 수 없는 수를 보통은 소수, prime number라고 얘기한다. 이것을 추상적인 대수에 대해서도 적용하기 위해서 irreducible, prime이라는 개념을 아래와 같이 정의한다. (1)은 어떤 수를 더 이상 나눌 수 없다는 의미이고, (2)는 ab를 r이 나누면 a 또는 b를 r이 나눈다는 의미인데, 아래 정의를 따르면 2,3,5.. 도 소수이지만, -2, -3, -5도 정수의 체계에서는 소수이다. 즉, 우리가 흔히 알고 있는 자연수의 소수와는 미묘한 차이가 있다.
정수 ring Z의 경우에는 irreducible 이면 prime이고, 그 반대도 성립한다. 일반적인 integral domain에서 r이 prime이면 irreducible임은 쉽게 보일 수 있다. 이는 r=ab→rab→ra w.l.o.g→r=(rk)b=r(kb) →r(1-kb)=0→kb=1→b is unit 이기 때문이다.
그러나 반대로 irreducible이면 prime 은 항상 성립하는 것은 아니다. 예를 들면 Z[√(-5)] 에서, 9=3x3=(2-√(-5)(2+√-5) 이며, 3은 irreducible이지만, 3이 (2-√(-5) 와 (2+√-5) 중 어느 것도 나누지는 못하기 때문이다.
그러나 ring R이 PID라면 그 둘은 동일하다. Z는 PID이기에 그 둘은 동일하다. 증명: Assume r is irreducible and rab and r is not divisor of a, we will show that rb. R is PID → rR+aR is principle ideal → r is irreducible means rR+aR=R → rx+ay=1 → r(xb)+(ab)y=b and rab → rb. 이제 추상적인 공간에서 더 이상 나눌 수 없다와 소수의 개념이 도입되었다. 그 다음은 추상적인 공간에서의 소인수 분해 개념의 도입이 필요할 것이다.
Integral domain (ID) R에서, r∈R인 수가 r~(p1)(p2),…,(pn) 이고, p1~pn들이 모두 irreducible 이라면 이것이 irreducible factorization이다. R의 모든 원소에 대해서 이러한 factorization이 associates 관계를 동일한 것으로 볼 때 유일하게 표현된다면, R 을 unique factorization domain (UFD)라고 부른다. 즉, r~(p1)(p2),…,(pn) 이고 r~(q1)(q2),…,(qn) 라면, 그 둘 사이는 equivalence iso-morphism이 존재해야 한다.
정수 환, Z는 UFD이다. 예를 들어 12=3x2x2=(-3)x(-2)x2 로 얼핏 보면 2가지 factorization 이 존재하는 것 같지만, 정수의 unit={1,-1}이므로 3~(-3)이고, 따라서 그 둘은 동일한 것으로 취급할 수 있기 때문이다. 모든 field는 UFD이다. Field는 모든 원소들이 unit이기 때문이다. 또한, 모든 PID는 UFD이다.
증명: R is PID, x ∈ R is such that x=(a1)(b1) a1 and/or b1 is irreducible. If a1 is irr.. then a1=a2b2 and a2 is irr.. then, a1∈(a2) and (a1) ⊂ (a2) .. continuing this means (a1) ⊂ (a2) ⊂ (a3) …
(a1)∪(a2) ∪…=R=(a) for some a since R is PID. But, a⊂(an) for some n so this process cannot continue. This is called as ascending chain condition (ACC). (Simple speaking: since PID satisfies ACC, factorizaton exists.) Uniqueness proof is skipped.
위의 증명에서 Ring내의 ideal chain I1⊂I2⊂… 이 finite sequence 내에서 중단될 수 있다면, 즉, I1⊂I2⊂…⊂In=I_{n+1}=I_{n+2}.. 라면 그러한 ring을 Noetherian ring이라고 부른다. 즉, Noetherian ring은 ACC 조건을 만족하는 ring이다. Left ideals에 대해서만 ACC가 성립되면 left-Noetherian이라고 하고, 반대로 right ideals에 대해서만 성립하면 right… 라고 하고, 둘다 성립하면 Noetherian 이라고 부른다. 물론, commutative ring이라면 그left N=right N=N으로 그 세개는 모두 동일하다. Noetherian에서 다음 세 조건은 동치이다.
(1) Every ascending chain of ideals is stationary (ACC)
(2) Every nonempty set of ideals of A has a maximal element
(3) Every ideal of I is finitely generated.
간략증명:
(1) → (2) I1⊂I2⊂…⊂In 이므로 In이 maximal element이다.
(2) → (3) Let J=max ideal finitely generated⊂I. Then for a∈I/J, (a)+J is finitely generated and J⊂(a)+J, contradiction.
(3) → (1) let I= I1∪I2∪…=(a1,a2,..,an). Since n is finite, a1~an∈I_m for some m. I⊂Im means ACC.
Noetherian ring은 PID의 개념을 확장한 것으로 이해할 수 있다. PID에서 모든 ideal I=(a)이므로 generator가 1개인데 반해, Noetherian에서는 generator가 여러 개 존재할 수 있다, 즉, ideal I=(a) + (b) + (c) 가 될 수 있다. Noetherian ring R이 주어진 경우, 이를 확장하여 여전히 Noetherian인 새로운 ring을 만들 수 있다. 이것을 Hilbert’s Basis theorem이라고 한다. 예를 들면, R[x], 즉 Noetherian R을 계수로 가지는 다항식 ring의 경우가 그러하다.
Gaussian integer Z[i]= Z[i]={a+b(i) a,b ∈ Z} 가 Euclidean domain(ED)임을 앞에서 보였다. ED이면 모든 ideal I에 가장 작은 수 n이 존재하고 I=(a)=aR이기에 PID 이다. 즉 ED→PID, ED⊂PID 이다. 또한 PID이면 UFD이기에, 즉 ED⊂PID⊂UFD 이기에 Z[i]는 또한 UFD이다.
그러나, 이것을 조금 수정하여 Z[2i]={a+b(2i) a,b ∈ Z} = {Gaussian integer with even imaginary part} 는 UFD가 아니다. -4=(2)x(-2)=(2i)x(2i) 인데, 2 와 2i 모두 irreducible이지만 그 둘이 associate 관계는 아니기 때문이다 (i 가 Z[2i]의 원소가 아니기에 associate관계가 아님). Z[√-5]]={a+b√(-5) a,b∈ Z} 도 6=(2)(3)=(1+√(-5))(1-√(-5)) 이고, 각각이 associate관계가 아니므로 UFD가 아니다.
===========================
12. GCD domain, Bezout domain
UFD 에서는 어떤 수이든 equivalence 관계를 고려하면 유일하게 더 이상 나눌수 없는 수들의 곱으로 나타낼 수 있다. 이것은 하나의 수의 관계이고, 만약 두개의 수 a,b가 있을 때, 이 둘의 gcd가 존재할 것인가라는 것은 다른 질문일 것이다. 집합 내 어떤 두 원소 사이에도 GCD가 존재할 때 이러한 대수 구조를 GCD domain이라고 부른다. 모든 UFD는 GCD domain에 속한다.
증명: a,b∈ some UFD R. a=u(a1)(a2)…(ar), b=v(b1)(b2)…(bs) where u,v are units and ai, bi’s are irreducibles. If we arrange well, then we can make (a1a2..at) are associates of (b1b2…bt) and there’s no further associates. Then we claim d=(a1a2..at)~(b1b2…bt) is gcd of a and b. d is common divisor since da, db. If f>d is another common divisor then, there should be some irreducible g which doesn’t belong to (a1~at) or (b1~bt) but divisor of a and b. That means g belongs to (a1~ar) and (b1~bs) meaning another associate exist. Contradiction.
I, J가 ideal 이면 I+J, IJ 가 모두 ideal이다. 그러면 I=aR, J=bR이 2개의principle ideal일 때, 즉, I+J=cR인 principle idea이냐하면 항상 그렇지는 않은데, 그것이 성립하는 경우 그러한 대수 구조를 Bezout domain 이라고 부른다. PID이면 당연히 그 안의 모든 ideal이 principle ideal이 된다는 것이 정의이므로 Bezout domain이다. Bezout domain의 두 정의는 1. A Bézout domain is an integral domain in which the sum of two principal ideals is again principal. 2. A Bézout domain is an integral domain in which every finitely generated ideal is principal. 이다.
Bezout domain에서 두 수 a, b가 있을 때, aR+bR=cR인 c가 존재하는데, aR⊂aR+bR=cR이므로 ca 이어야 하고, 같은 방법으로 cb이어야 하므로, c는 a와 b의 공약수이다. 그 중 가장 큰 것을 gcd라고 하면 Bezout domain에서는 어떤 두 수 사이에도 gcd가 존재하고 그 gcd d=ax+by 라는 Bezout identity로 주어진다. 즉, a와 b의 최대 공약수는 두 수의 linear combination으로 표현된다.
이것은 단순히 gcd가 존재한다는 것보다는 더 강한 조건이기에 Bezout domain → GCD domain이지만 그 반대는 아니다. 예를 들면 Z[x]는 GCD가 존재하지만 Bezout identity는 성립하지 않는다. 예를 들면 gcd{(x-2)(x-3), (x-1)(x-2)}=(x-1) 이지만 그 둘의 곱으로 표시할 수는 없다. 같은 원리로 모든 UFD가 Bezout는 아니다. 또한 Bezout domain이면서 UFD가 아닐 수도 있다. 예를 들면, ring of all algebraic integers (정수 계수 다항식의 복소수 해들의 집합)는 Bezout domain 이지만 UFD는 아니다(증명은 복잡).
UFD이면 GCD domain이지만, GCD domain은 항상 UFD일 필요는 없다. Factorization 이 유일하지 않은데, gcd가 존재한다는 것이 조금 이상하게 들릴지 모른다. 예를 들면, ring of all algebraic integers (정수계수 다항식의 해들의 집합)는 Bezout domain 이고 따라서 GCD domain이지만 UFD는 아니다.
Bezout domain R에서 다음은 동치의 조건들이다.
(1). R is a principal ideal domain.
(2). R is Noetherian.
(3). R is a unique factorization domain (UFD).
(4). R satisfies the ascending chain condition on principal ideals (ACCP).
(5). Every nonzero nonunit in R factors into a product of irreducibles (R is an atomic domain).
마지막으로 각 ring 구조들간의 계층을 살펴보면,
(1) Field ⊂ ED ⊂ PID ⊂ UFD ⊂ GCD domain ⊂ ID ⊂ Commutative rings ⊂ rings.
(2) Field ⊂ ED ⊂ PID ⊂ Bezout domain ⊂ GCD domain ⊂ ID ⊂ Commutative rings ⊂ rings
그러나 반대로 irreducible이면 prime 은 항상 성립하는 것은 아니다. 예를 들면 Z[√(-5)] 에서, 9=3x3=(2-√(-5)(2+√-5) 이며, 3은 irreducible이지만, 3이 (2-√(-5) 와 (2+√-5) 중 어느 것도 나누지는 못하기 때문이다.
그러나 ring R이 PID라면 그 둘은 동일하다. Z는 PID이기에 그 둘은 동일하다. 증명: Assume r is irreducible and rab and r is not divisor of a, we will show that rb. R is PID → rR+aR is principle ideal → r is irreducible means rR+aR=R → rx+ay=1 → r(xb)+(ab)y=b and rab → rb. 이제 추상적인 공간에서 더 이상 나눌 수 없다와 소수의 개념이 도입되었다. 그 다음은 추상적인 공간에서의 소인수 분해 개념의 도입이 필요할 것이다.
Integral domain (ID) R에서, r∈R인 수가 r~(p1)(p2),…,(pn) 이고, p1~pn들이 모두 irreducible 이라면 이것이 irreducible factorization이다. R의 모든 원소에 대해서 이러한 factorization이 associates 관계를 동일한 것으로 볼 때 유일하게 표현된다면, R 을 unique factorization domain (UFD)라고 부른다. 즉, r~(p1)(p2),…,(pn) 이고 r~(q1)(q2),…,(qn) 라면, 그 둘 사이는 equivalence iso-morphism이 존재해야 한다.
정수 환, Z는 UFD이다. 예를 들어 12=3x2x2=(-3)x(-2)x2 로 얼핏 보면 2가지 factorization 이 존재하는 것 같지만, 정수의 unit={1,-1}이므로 3~(-3)이고, 따라서 그 둘은 동일한 것으로 취급할 수 있기 때문이다. 모든 field는 UFD이다. Field는 모든 원소들이 unit이기 때문이다. 또한, 모든 PID는 UFD이다.
증명: R is PID, x ∈ R is such that x=(a1)(b1) a1 and/or b1 is irreducible. If a1 is irr.. then a1=a2b2 and a2 is irr.. then, a1∈(a2) and (a1) ⊂ (a2) .. continuing this means (a1) ⊂ (a2) ⊂ (a3) …
(a1)∪(a2) ∪…=R=(a) for some a since R is PID. But, a⊂(an) for some n so this process cannot continue. This is called as ascending chain condition (ACC). (Simple speaking: since PID satisfies ACC, factorizaton exists.) Uniqueness proof is skipped.
위의 증명에서 Ring내의 ideal chain I1⊂I2⊂… 이 finite sequence 내에서 중단될 수 있다면, 즉, I1⊂I2⊂…⊂In=I_{n+1}=I_{n+2}.. 라면 그러한 ring을 Noetherian ring이라고 부른다. 즉, Noetherian ring은 ACC 조건을 만족하는 ring이다. Left ideals에 대해서만 ACC가 성립되면 left-Noetherian이라고 하고, 반대로 right ideals에 대해서만 성립하면 right… 라고 하고, 둘다 성립하면 Noetherian 이라고 부른다. 물론, commutative ring이라면 그left N=right N=N으로 그 세개는 모두 동일하다. Noetherian에서 다음 세 조건은 동치이다.
(1) Every ascending chain of ideals is stationary (ACC)
(2) Every nonempty set of ideals of A has a maximal element
(3) Every ideal of I is finitely generated.
간략증명:
(1) → (2) I1⊂I2⊂…⊂In 이므로 In이 maximal element이다.
(2) → (3) Let J=max ideal finitely generated⊂I. Then for a∈I/J, (a)+J is finitely generated and J⊂(a)+J, contradiction.
(3) → (1) let I= I1∪I2∪…=(a1,a2,..,an). Since n is finite, a1~an∈I_m for some m. I⊂Im means ACC.
Noetherian ring은 PID의 개념을 확장한 것으로 이해할 수 있다. PID에서 모든 ideal I=(a)이므로 generator가 1개인데 반해, Noetherian에서는 generator가 여러 개 존재할 수 있다, 즉, ideal I=(a) + (b) + (c) 가 될 수 있다. Noetherian ring R이 주어진 경우, 이를 확장하여 여전히 Noetherian인 새로운 ring을 만들 수 있다. 이것을 Hilbert’s Basis theorem이라고 한다. 예를 들면, R[x], 즉 Noetherian R을 계수로 가지는 다항식 ring의 경우가 그러하다.
Gaussian integer Z[i]= Z[i]={a+b(i) a,b ∈ Z} 가 Euclidean domain(ED)임을 앞에서 보였다. ED이면 모든 ideal I에 가장 작은 수 n이 존재하고 I=(a)=aR이기에 PID 이다. 즉 ED→PID, ED⊂PID 이다. 또한 PID이면 UFD이기에, 즉 ED⊂PID⊂UFD 이기에 Z[i]는 또한 UFD이다.
그러나, 이것을 조금 수정하여 Z[2i]={a+b(2i) a,b ∈ Z} = {Gaussian integer with even imaginary part} 는 UFD가 아니다. -4=(2)x(-2)=(2i)x(2i) 인데, 2 와 2i 모두 irreducible이지만 그 둘이 associate 관계는 아니기 때문이다 (i 가 Z[2i]의 원소가 아니기에 associate관계가 아님). Z[√-5]]={a+b√(-5) a,b∈ Z} 도 6=(2)(3)=(1+√(-5))(1-√(-5)) 이고, 각각이 associate관계가 아니므로 UFD가 아니다.
===========================
12. GCD domain, Bezout domain
UFD 에서는 어떤 수이든 equivalence 관계를 고려하면 유일하게 더 이상 나눌수 없는 수들의 곱으로 나타낼 수 있다. 이것은 하나의 수의 관계이고, 만약 두개의 수 a,b가 있을 때, 이 둘의 gcd가 존재할 것인가라는 것은 다른 질문일 것이다. 집합 내 어떤 두 원소 사이에도 GCD가 존재할 때 이러한 대수 구조를 GCD domain이라고 부른다. 모든 UFD는 GCD domain에 속한다.
증명: a,b∈ some UFD R. a=u(a1)(a2)…(ar), b=v(b1)(b2)…(bs) where u,v are units and ai, bi’s are irreducibles. If we arrange well, then we can make (a1a2..at) are associates of (b1b2…bt) and there’s no further associates. Then we claim d=(a1a2..at)~(b1b2…bt) is gcd of a and b. d is common divisor since da, db. If f>d is another common divisor then, there should be some irreducible g which doesn’t belong to (a1~at) or (b1~bt) but divisor of a and b. That means g belongs to (a1~ar) and (b1~bs) meaning another associate exist. Contradiction.
I, J가 ideal 이면 I+J, IJ 가 모두 ideal이다. 그러면 I=aR, J=bR이 2개의principle ideal일 때, 즉, I+J=cR인 principle idea이냐하면 항상 그렇지는 않은데, 그것이 성립하는 경우 그러한 대수 구조를 Bezout domain 이라고 부른다. PID이면 당연히 그 안의 모든 ideal이 principle ideal이 된다는 것이 정의이므로 Bezout domain이다. Bezout domain의 두 정의는 1. A Bézout domain is an integral domain in which the sum of two principal ideals is again principal. 2. A Bézout domain is an integral domain in which every finitely generated ideal is principal. 이다.
Bezout domain에서 두 수 a, b가 있을 때, aR+bR=cR인 c가 존재하는데, aR⊂aR+bR=cR이므로 ca 이어야 하고, 같은 방법으로 cb이어야 하므로, c는 a와 b의 공약수이다. 그 중 가장 큰 것을 gcd라고 하면 Bezout domain에서는 어떤 두 수 사이에도 gcd가 존재하고 그 gcd d=ax+by 라는 Bezout identity로 주어진다. 즉, a와 b의 최대 공약수는 두 수의 linear combination으로 표현된다.
이것은 단순히 gcd가 존재한다는 것보다는 더 강한 조건이기에 Bezout domain → GCD domain이지만 그 반대는 아니다. 예를 들면 Z[x]는 GCD가 존재하지만 Bezout identity는 성립하지 않는다. 예를 들면 gcd{(x-2)(x-3), (x-1)(x-2)}=(x-1) 이지만 그 둘의 곱으로 표시할 수는 없다. 같은 원리로 모든 UFD가 Bezout는 아니다. 또한 Bezout domain이면서 UFD가 아닐 수도 있다. 예를 들면, ring of all algebraic integers (정수 계수 다항식의 복소수 해들의 집합)는 Bezout domain 이지만 UFD는 아니다(증명은 복잡).
UFD이면 GCD domain이지만, GCD domain은 항상 UFD일 필요는 없다. Factorization 이 유일하지 않은데, gcd가 존재한다는 것이 조금 이상하게 들릴지 모른다. 예를 들면, ring of all algebraic integers (정수계수 다항식의 해들의 집합)는 Bezout domain 이고 따라서 GCD domain이지만 UFD는 아니다.
Bezout domain R에서 다음은 동치의 조건들이다.
(1). R is a principal ideal domain.
(2). R is Noetherian.
(3). R is a unique factorization domain (UFD).
(4). R satisfies the ascending chain condition on principal ideals (ACCP).
(5). Every nonzero nonunit in R factors into a product of irreducibles (R is an atomic domain).
마지막으로 각 ring 구조들간의 계층을 살펴보면,
(1) Field ⊂ ED ⊂ PID ⊂ UFD ⊂ GCD domain ⊂ ID ⊂ Commutative rings ⊂ rings.
(2) Field ⊂ ED ⊂ PID ⊂ Bezout domain ⊂ GCD domain ⊂ ID ⊂ Commutative rings ⊂ rings
반응형
Comments