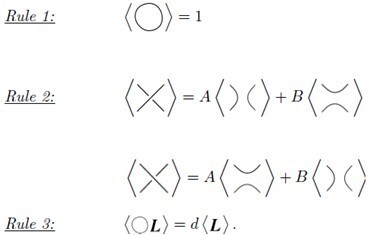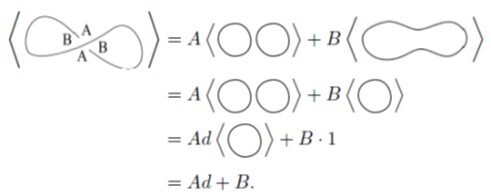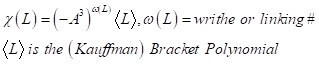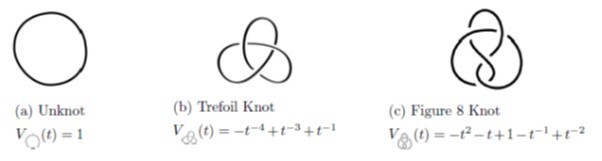매듭이론

Edward Witten 은 뉴질랜드 수학자 Jones와 함께 1990년, 수학계의 노벨상인 Fields medal을 수상한다. 올림픽처럼 4년마다, 40세 이하에게만 수여되기에 세상에서 가장 유명한 문제를 풀었다고 하는 와일스도 41세의 나이로 수상을 실패한(대신 fields 특별상 수상) 그 상을, 당대 쟁쟁한 수학자들을 모두 물리치고 수상한다. 전무후무한 일이며, 향 후로도 그런 일이 생길 것 같지는 않다. 수학자들의 자존심이 걸린 문제이기도 하기 때문이다. 그들의 공통된 업적은 knot theory에 관한 것이다.

Knot(매듭) K는 3차원 공간의 closed curve를 말한다. 수학적으로는 “smooth embedding of the one sphere S1 onto R³”라고 한다. 2개의 knot는 3차원 공간의 smooth deformation 에 의해서 변환 관계에 있을 때 동일한 것으로 간주된다. 즉, “Two knots K and K’ are called isotopic if K is obtained from K’ by a continuous deformation such that there is no self-interaction at any time during deformation.” 만약 여러 개의 circle들이 고리처럼 얽혀 있다면 이것을 link라고 부른다.

그러나 손으로 매듭을 푸는 것과 같은 smooth deformation을 수학적으로 어떻게 다룰 것인지는 쉬운 문제는 아니며 3차원 공간에서 복잡하게 얽힌 여러 모양들을 우리가 직관적으로 쉽게 이해하기가 쉽지는 않다. 실제로 3차원 공간에서 얽힌 실을 2차원 공간에 투영할 수 있다. 이 때, 실의 한 부분은 다른 부분을 위로 혹은 아래로 지나갈 수가 있을 것이다. 교차점의 수에 따라 가능한 매듭의 종류는 빠르게 늘어나서, 16개의 교차점에서는 이미 100만개를 넘어선다. 그들이 서로 다른 type인지 혹은 isotopy인지를 어떻게 체계적으로 알아낼 것인가?

• 

2 부분이 교차되면서 지나가는 모든 부분을 서로 겹치지 않게 늘어놓으면, 3차원 공간에서 매듭이 어떻게 얽혀있는지를 2차원 공간에 그릴 수 있다. 아래에 몇 가지 예시를 그려놓았다. 아래의 세 모양은 모두 다른 매듭처럼 보이지만, 실제로 잘 풀어보면 모두 왼쪽의 원처럼 풀리게 되어 있다. 이 3개의 서로 다른 모양의 매듭이 실제로 동형의 원인지, 아니면 다른 복잡하게 얽힌 모양인지를 어떻게 알 수 있을까? 이것을 연구하는 분야가 바로 knot theory이다.

• 

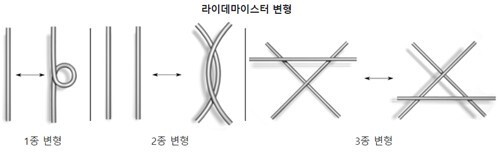
Kurt Reidemeister는 1927년에 서로 isotopy (동형)인 두 매듭은 아래와 같은 세가지 동작들의 연결에 의해서 이루어진다고 증명하였다. 아래 3가지를 각각 R1, R2, R3 Reidemeister moves 라고 부른다.
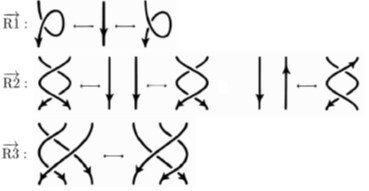
R1: twist or untwist in either direction
R2: Move one loop completely over another
R3: Move a loop completely over or under a crossing

• 

이렇게 2차원에 projection 된 knot Reidemeister moves에 방향성을 부여할 수 있는데, 이것을 oriented Reidemeister moves라고 한다.

• 

또한 교차점에서 “left pass under right”로 지나가면 +를 반대로 “left pass over right”이면 -의 부호를 부여할 수 있다. 즉, 아래에서 왼쪽 그림은 +, 오른쪽 그림은 -의 부호를 부여한다. 이러한 부호를 모두 합한 것을 그 diagram의 linking number라고 부른다. 아래 그림의 linking numer는 2이다. Linking number(writhe라고도 한다)는 isotopy 에 대해서 불변량이다. 즉, 아래 그림에 Reidemesiter move를 가하여도 그 값은 불변이다.

• 

1990년 Louis Kauffman은 매듭들을 분류할 수 있는 중요한 불변 다항식, Kauffman polynomial 을 제안한다. 이것으로부터 곧이어 소개할 Jones polynomial을 유도할 수 있다. Kauffman 다항식을 설명하기 전에 먼저 Kauffman bracket 혹은 Bracket 다항식을 설명한다. 내용을 어떻게 유도했는지는 복잡하겠지만, 다항식을 구하는 규칙은 간단히 아래 그림으로 설명할 수 있다.
첫번째 룰은, 그냥 독립된 원의 경우 Kauffman bracket < O >값은 1이다. 두번째 룰에 따라, 교차점의 경우 교차점을 수직과 수평 방향으로 분리하면서 각 backet의 값에 A와 B값을 곱한다. 마지막 룰은, diagram이 원과 다른 diagram으로 분리되면 d를 bracket <L>에 곱한다.

• 

간단한 예시를 살펴보자. 좌측 매듭에 대한 Bracket 다항식은 아래와 같다. 아래는 아직 다항식 같지는 않아 보이는데, 이것은 d와 B값이 정해지지 않아서이다. 그 값이 무엇인지는 곧 설명한다.

• 

좀 더 복잡한 예로는 Trefoil knot라고 불리는 아래 예가 가능하다.

• 

이제 B와 d를 A로 표시해 보자. 우리가 원하는 관계는 아래 그림과 같이 하나의 선위에 다른 선이 놓인 경우 그들을 분리해도 동일한 결과를 얻고 싶다. 즉, knot invariant 한 형태가 되기를 원한다. 아래 그림을 Kauffman rule에 따라서 분리하면, 좌측 그림은 4개의 그림으로 분리되고 식으로는 A^2+ABd+ABd+B^2=d 라는 수식을 얻는다. 따라서, B=A^-1, d=-(A^2+A^-2)으로 두면 위의 식을 만족한다. 그 조건에 따라, 다시 Kauffman rule을 적어보면 아래와 같다.

• 

• 

Kauffman bracket의 경우, Type II, Type III Reidemeister move에 대해서는 불변이지만, Type 1에 대해서는 불변이 아닌데, 아래와 같이 Kauffman 다항식을 정의하면 모든 변환에 대해서 불변이 된다.

• 

==========================

1984년 Vaughan Jones는 불변 다항식인 Jones polynomial을 발표한다. 앞서 정의한 Kauffman polynomial에서 A자리에 t^(-1/4)를 넣으면 나오는 다항식이며, 결과적으로 t^1/2 과 t^-1/2 로 생성되는 다항식이다. 이것은 다음과 같은 skein relation 이라고 불리는 관계식에 따라 기술된다.

• 

매듭을 거울에 비추면 나타나는 매듭은 아래 수식에서 t자리에 t^-1을 넣으면 된다. 그런데, L+의 mirror image가 L- 이므로 그 값이 바뀌지 않는다. 즉, Jones 다항식은 매듭의 단순한 거울 대칭을 동일한 것으로 인식하는 장점이 있다. 이것을 achairal 혹은 amphicheiral knot라고 부른다. 반면에 거울 대칭을 다른 매듭으로 인식하면 이것은 chairal knot이다.

Jones 다항식이 다르면 그들은 다른 종류의 매듭이다. 그러나, 불행히도 Jones 다항식이 동일하다고 해서 그들이 같은 종류의 매듭은 아니다. Jones 다항식의 몇가지 예는 아래와 그림과 같다.

• 

1988년 20세기 최고의 수학자 중 한명인 Michael Atiyah (아티야 싱어 정리로 유명하다)는 1988년 열린 Hermann Weyl 수학 심포지엄에서 두가지 문제를 제시한다. 하나는 Donaldson theory 에서 제시하는 불변량의 물리학적인 의미는 무엇인가이고 두번째는 위에서 설명한 매듭이론의 Jones 다항식의 3차원적인 정의(앞서의 정의는 다분히 3차원 매듭이 2차원에 투영된 diagram에서 정의되었다)가 무엇이고, 그 물리학적인 의미는 무엇인가라는 문제였다.

에드워드 위튼은 1989년 “Quantum Field Theory and the Jones Polynomial”라는 논문에서 그 두가지 질문 모두에 대한 답을 제시하면서, TQFT (topological quantum field theory)라는 새로운 학문 분야를 개척한다. 1986년 Fields medal은 Donaldson(팔팅스, 프리드먼과 3인 공동)이, 1990년 Fields medal은 Jones와 Witten(디린펠트, 모리 시레후미도 공동)이 수상한다.