자신을 인식하는 물질, 존재와 의식... 자연철학적 접근
위상공간 본문
위상공간에서 “connected space”라고 하면, 그 공간을 2개이상의 disjoint non-empty open subset의 합집합으로 표현할 수 없을 때를 말한다.
만약 위상 공간 내 임의의 두 점 x, y 를 연결하는 연속 함수 f : I → X, I=[0,1] unit interval 가 존재하는 경우, 그 공간은 “path-connected space”라고 한다.
Path-connected → connected이지만 그 반대는 아니다. 그 예를 찾기가 쉽지는 않지만, 수학책에 자주 나오는 예가 아래 그림의 위상 정현파 곡선 (topologist sine curve)이다. 아래 그림의 곡선은 S={(x,sin(1/x)): 0<x<1}∪{(0,0)} 로 주어진다.
만약 위상 공간 내 임의의 두 점 x, y 를 연결하는 연속 함수 f : I → X, I=[0,1] unit interval 가 존재하는 경우, 그 공간은 “path-connected space”라고 한다.
Path-connected → connected이지만 그 반대는 아니다. 그 예를 찾기가 쉽지는 않지만, 수학책에 자주 나오는 예가 아래 그림의 위상 정현파 곡선 (topologist sine curve)이다. 아래 그림의 곡선은 S={(x,sin(1/x)): 0<x<1}∪{(0,0)} 로 주어진다.
Sin(1/x)는 (0,1] 에서 연속 함수이므로 (x,sin(1/x))는 (0,1]에서 connected이고, 만약 A가 connected이면, closure(A)도 connected라는 성질을 이용하면(증명 생략), 곡선 S는 connected space이다. 그러나, S는 path-connected space는 아니다.
만약 path-connected가 되려면, 곡선위의 두 점 (t,sin(1/t))와 (0,0)을 연결하는 연속함수 f가 존재해야 한다. 연속함수는 convergent sequence an에 대해서 f(lim an)=lim f(an)이라는 성질을 만족해야 하는데, n이 무한대로 가면 lim 1/(π/2+2πn)=0인데, lim f(an)=sin(π/2+2πn)=1이기 때문에 그러한 연속함수는 존재하지 않고 따라서 path-connected가 아니다.
Topologist curve 의 다른 확장된 형태로 Warsaw circle 혹은 Polish circle이라고 불리는 connected, but not path-connected 곡선이 있다 (1968, Karol Borsuk가 제시). W= {(x,sin(π/x)): 0<x<1}∪{(0,y)-1<=y<=1} ∪ C(ircle) 로 주어지며 아래 그림과 같다. 이것들은 S1(원)과 homotopy 인 것 같지만, 실제로는 그렇지 않다. 또한 이 곡선은 얼핏 보기에는 한 점으로 contraction이 가능할 것 같지만, 그렇지 않은 예로 수학책에 자주 등장한다.
그 둘보다 좀 더 강한 연결은 “arcwise-connected or arc-connected space”인데, arc에서 보듯이 이것은 좀 더 부드럽게 연결되는 의미로 path-connected 에서의 연속함수가 continuous inverse, 즉 연속인 역함수도 존재하는 경우에 즉 [0,1]에서 X로도, X 에서 [0,1]로도 상호 변환이 가능할 때 혹은 f 가 continuous이면서 injective일때를 말한다. 실제로 어떤 책들은 arcwise connected = path connected로 사용하기도 한다. 만약 topological space X가 uncountable이라면 그 둘은 동일한 의미인 것으로 보인다.
만약 위상 공간 X의 모든 점들이 path-connected이고, 두 점을 잊는 모든 path가 homotopy 관계일 때, X가 simply connected라고 한다. 혹은, 위상 공간 X가 path-connected이고, 모든 loop를 한점으로 contraction 할 수 있을 때 X가 simply connected라고 얘기한다. Fundamental group은 위상공간이 simply connected에서 얼마나 벗어나는지를 알려준다.
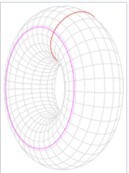
Simply connected 라면 fundamental group π(x)={e}, 즉 trivial group이다. π(S1)=π(circle)=Z 이고, S1은 path connected이지만, simply connected 는 아니다 (원 위에 loop를 한 점으로 만들 수 없다). 반면 D2, 즉 속이 꽉찬 disk의 경우, path connected 이고 모든 loop을 그 공간내에서 한점으로 만들 수 있기에 simply connected space이다. 아래에서 구의 표면, S2공간은 simply connected
이고, Torus=S1xS1의 경우 simply connected가 아니다.
만약 위상 공간 X의 모든 점들이 path-connected이고, 두 점을 잊는 모든 path가 homotopy 관계일 때, X가 simply connected라고 한다. 혹은, 위상 공간 X가 path-connected이고, 모든 loop를 한점으로 contraction 할 수 있을 때 X가 simply connected라고 얘기한다. Fundamental group은 위상공간이 simply connected에서 얼마나 벗어나는지를 알려준다.
Simply connected 라면 fundamental group π(x)={e}, 즉 trivial group이다. π(S1)=π(circle)=Z 이고, S1은 path connected이지만, simply connected 는 아니다 (원 위에 loop를 한 점으로 만들 수 없다). 반면 D2, 즉 속이 꽉찬 disk의 경우, path connected 이고 모든 loop을 그 공간내에서 한점으로 만들 수 있기에 simply connected space이다. 아래에서 구의 표면, S2공간은 simply connected
이고, Torus=S1xS1의 경우 simply connected가 아니다.
==========================
위상공간은 어떤 집합 X와 U⊂X 이며 finite intersection 과 arbitray union(could be infinite or uncountable) 에 대해서 닫혀있는 열린집합(open set)들의 집합 U로 구성된 공간을 말한다. 일반적인 위상공간에서의 homomorphism (보통은 f(x+y)=f(x)+f(y)로 정의)은 위상 공간에서는 continuous function 으로 정의된다. 위상공간에서 연속 함수는, f:X→Y에서 U_y⊂Y일 때, f^(-1)(U_y) ⊂ U_x, 즉 열린집합의 preimage가 열린집합일 때를 의미한다.
위상공간 X의 한 점 p의 (open) neighbourhood 란, 그 안에 p를 포함하는 open set U(p)를 포함하는 부분집합 N(p)를 말한다. 즉, p∈U(p) ⊂ N(p) ⊂ X이다. 보통은 N(p)=U(p), 즉 p점을 포함하는 open set을 의미하지만 N(p)는 반드시 open 일 필요는 없으며, 만약 open set인 경우 open neighbourhood라고 부른다. 책에 따라서는 open neighbourhood를 그냥 neighbourhood라고 하는 경우도 있다. Metric이 정의된 공간의 경우는 보통 Br(p)={x∈X, d(x,p)<r}인 open ball을 잡는다.
위상공간 (X,U)의 한 점 x의 Neighbourhood basis 혹은 local basis란, neighbourhood 의 집합 B인데, 그 점 주위의 어떤 neighbourhood를 잡더라도, 그 안에 B의 원소에 해당하는 neighbourhood를 포함하는 경우를 의미한다. 말이 좀 어렵다. For each neighbourhood N of x, there is an M∈B such that M⊂ N. 예를 들어, 실수 공간 R의 원점 0은, B={(-1/n, 1/n)} 이라는 basis가 존재며, 원점 주위에 어떤 neighbourhood를 잡더라도 (-1/n, 1/n)인 neighbourhood를 잡을 수 있기에 원점에서 basis를 가진다고 얘기한다.
만약 위상공간 X의 모든 점들이 neighbourhood basis B를 가지고, B가 connected open subset이라면, 그 공간을 locally connected라고 부른다. 위상공간에서 이와 관련한 아래 3가지 명제들은 서로 동치 관계이다(증명은 생략).
앞서 설명한 topologists sine curve, Warsaw(Polish) curve는 모두 connected space이지만, locally connected space는 아니다. (0,0)의 주변에 어떤 neighbourhood를 잡더라도, 그 구간을 확대해 보면, 연결되지 않은 수많은 곡선들이 지나가기에 locally connected space가 아니다.
반응형
Comments