자신을 인식하는 물질, 존재와 의식... 자연철학적 접근
양자 역학의 태동 1- 흑체 복사 본문
blackbody(흑체)는 말 그대로 모든 주파수나 입사각의 전자기 복사를 흡수하는 이상적인 물체이다. 에너지를 흡수하면 blackbody의 온도는 올라가고 주변과 열평형상태를 이룬다. 이 상태에서 흑체는 자체적으로 다시 열을 방출한다. 즉, 입사된 전자기파가 아니라, 자체적으로 온도에 따른 전자기 복사 형태로 에너지를 배출한다. 방출하는 형태는 Planck’s law라고 부르는 법칙에 따라서이다. 양자역학의 태동에 있어서, 흑체 복사이론은 중요한 역할을 수행하였다. 흑체는 전도체의 표면에 작은 구멍을 내는 형태로 만들 수 있다. 가장 완벽한 흑체는 cosmic microwave background이다.
흑체가 LxLxL의 cubical box형태라고 가정하자. Box는 fixed, rigid, perfectly conducting wall로 이루어졌다고 가정하자. 따라서 표면에서 전자기파는 존재하지 않는다. 즉, 경계에서 E/H field=0이다. 이러한 경계조건을 만족하려면, 흑체 내부의 전자기파의 파장은 반파장의 배수형태가 가능하다. 즉,


이제 운동량 혹은 k 공간을 pi/L 단위로 표시하면(k=pi/L*p) 위의 그림과 같이 정수점에 해당하는 격자의 전자기파만이 존재할 수 있다. P와 dp 사이의 에너지 상태의 수, 즉 상태 밀도를 구하기 위해서는 거리 p와 p+dp사이에 존재하는 상태의 수를 세어야 하는데, 이를 위해서 약간의 trick, 가정을 해 보자. 즉, 거리 p내에 있는 점들의 수는 반경 p인 구의 체적과 동일하다고 가정하자. 점이 하나 더해질 때 마다 부피가 1씩 증가하니, 이는 어느 정도 reasonable한 가정이고, 특히 p가 크면 오차가 거의 없다고 가정할 수 있을 것이다. 이제, 상태 밀도 함수를 p공간에서 구하면

이것을 Rayleigh Jean’s 공식이라고 부른다. 위의 공식은 낮은 에너지구간에서 실험식과 근사하지만 치명적인 문제점을 안고 있다. Ultraviolet catastrophy라고 부르는 현상이다.
앞서의 수식을 살펴보면 상태의 수가 주파수가 커짐에 따라 무한히 증가한다. 그런데, 통계역학의 기본 가정이, 평형상태에서 모든 가능한 degree of freedom들은 동일한 에너지를 나눠가진다. 즉, 자유도마다 혹은 가능한 상태마다 kT의 에너지를 가지게 되므로, 주파수당 에너지 밀도는 아래와 같고, 에너지 밀도는 주파수가 증가할 수도록 증가한다.

이제 모든 주파수에 대해서 에너지의 합을 구해보면

Blackbody 안의 에너지가 무한대가 존재한다는 결론에 도달한다. 물론, 이것은 실험결과와 동일하지 않다. Blackbody 의 온도가 일정한데, 에너지를 무한대 가질수 있다는 것은 말이 안된다 ^^
이제 이러한 모순점을 해결하도록 하자. Planck의 도발, 양자역학의 태동이다. 앞서의 모든 문제점의 시작은 에너지가 증가함에 따라 점유 가능한 상태의 수가 계속 늘어난다는데에 있다. 만약에.. 만약에 광자가 모든 에너지를 가질 수 없고, 특정 에너지의 배수의 에너지만 가질 수 있다면, 즉, 빛이 알갱이로 되어 있다면 어떨까? 사실, 아인슈타인의 광양자설은 Planck의 아이디어의 차용에 불과하다. 그는 Planck의 이론을 보고, “아하,, 이것을 광양자 문제에 적용하면 되겠구나”라고 생각하고 적용하고, 노벨상을 수상한다. 아이러니하다.
그러나 https://physicsworld.com/a/max-planck-the-reluctant-revolutionary/
를 보면, 실제로 플랑크는 흑체 복사 문제를 해결하고도 에너지의 양자화라는 부분에서 계속 머뭇거린다. 기존의 관습에 맞설 힘이 없었거나, 자신의 선입견에 너무 사로 잡혀 있었기 때문이다. 실제로 양자역학의 핵심적인 아이디어는 어린 아인슈타인이라고 위의 문서에서는 주장한다
어쨌던, Max planck는 흑체 복사 문제를 해결하기 위하여 광자는 주파수의 배수배에 해당하는 에너지 상태만 점유할 수 있다고 가정한다. 즉,
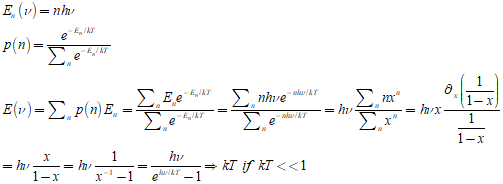
위에서 중요한 것은 주파수가 증가함에 따라 분모항이 지수적으로 증가하고, 따라서 그 주파수에 해당하는 에너지 밀도가 급격히 떨어진다는 것이다. 이것이, 주파수에 따른 체적의 증가분을 상쇄하면 흑체 복사를 완벽하게 묘사할 수 있다. 즉, 종합적인 에너지 밀도는

이제 총 에너지를 구해보면

이것을 Stefan-Boltzmann law라고 부른다.
위의 이야기의 핵심은 무엇인가.. 플랑크는 희안하게도, 누구도 양자역학을 얘기하지 않았는데, 빛이 파장이 아니라 기본적인 어떤 알갱이, 빛 알갱이 photon으로 되어 있다는 생각을 했다. 그리고는 자신의 생각을 부정한다. 어쨌던, 플랑크가 얘기한 얘기는 우리가 wave라고 생각한 것들이 실제로는 어떤 알갱이, quanta로 이루어져 있다는 것이다. 나중에, 드브로이는, 우리가 알갱이라고 부르는 그 무엇... 입자는 다시 wave라고 얘기한다. 양자 역학의 핵심은, 입자와 파동의 이중성... 이 세상 어떤 존재도 이해하기 힘든, 개념에 관한 ... 참으로 이상한 얘기에 관한 것이다.
'양자이론' 카테고리의 다른 글
| 통계역학-Ensemble에 대해 (0) | 2021.02.11 |
|---|---|
| 볼츠만 분포 (0) | 2021.02.10 |
| 통계역학 - 맥스웰 분포 (0) | 2021.02.09 |
| 에미뇌터와 대칭이론 (0) | 2021.02.08 |
| 양자역학의 태동 - 아인슈타인의 고체 비열 이론 (0) | 2021.02.01 |




