자신을 인식하는 물질, 존재와 의식... 자연철학적 접근
에미뇌터와 대칭이론 본문
물리학은 흔히들 대칭과 그에 따른 보존량을 얘기하는 학문이라고 한다. 물리학 이론을 전개할 때 가장 먼저 하는 일은, 어떤 대칭을 얘기할 것인가를 정하는 것이다. 전역 대칭, 즉 시공간의 모든 지점에 대해서 대칭이면 그것을 전역 대칭 (global symmetry)라고 하고, 각 지점마다 대칭이 별도로 존재하면 그것을 국부 대칭(local symmetry)라고 부른다. 전역 대칭에는 반드시 그에 상응하는 보존량이 존재한다.
움직이던 물체는 외력이 작용하지 않는 한 현재의 운동을 그대로 보존하는 방향으로 움직인다. 운동량의 보존의 법칙은 공간의 병행 대칭성, translation symmetry 가 존재하기 때문에 성립한다. 만약 시공간이 균일하게 설계되지 않았다면 얘기는 완전히 달라진다. 또한 우리가 흔히 에너지라고 부르는 양을 물리학자들은 time translation symmetry 의 생성자, 다른 말로 오늘의 물리 법칙이 어제도, 내일도 그대로 적용되기 때문에 나타나는 현상이라고 설명한다.
에미뇌터(1882~1935) 물리학계에서 가장 많이 언급되는 여성물리학자이다. 사실 노벨상을 두번 수상한 퀴리여사보다도 더욱 자주 만나게 되는 인물이다. 양자역학/양자장론/입자물리 공부에서 그녀의 이름을 피하기는 불가능하다. 역시 유대인이다. 유대인들과 인간들은 같은 종족인지 때로는 의심된다. 유대민족은 일반 민족보다 평균지능이 우수함을 부정할 수는 없다. 문화적 차이일 수도 있고, 유전적 차이일 수도 있다.

뇌터가 살던 시절은 아직 성적 평등이 이루어지지 않았다. 오늘날에는 게임중독과 사고의 단순함으로 인해서 남성들의 멸종을 걱정해야 하는 시기이지만, 그 당시에는 여성들의 사회활동, 특히 지적인 영역에서의 자리는 거의 존재하지 않았다. 철학사/수학사 전체를 통틀어 여성 철학자의 이름은 접하기 쉽지 않다. 한나 아렌트와 예전에 독서밴드하느라 접한 리베카 골드스타인, 그리고 신비적인 고대 여성 철학/수학인 히파티아(355-415) 정도이다. 뛰어난 수학실력과 박사학위가 있었지만, 대학강의는 허용되지 않았다. 가장 위대한 수학자 중 한 명인 힐버트(1862-1943)의 추천에 따라 강의를 맡을 때에도 여성이 교수가 되는 것을 모두가 공격했다.
에미뇌터의 가장 위대한 업적은 모든 전역 대칭에는 보존되는 물리량이 존재한다는 뇌터의 정리를 찾은 것이다. Continuous and global symmetries of the action imply conservation laws 가 그 내용이다. Emmy Noether 가 1918년에 증명한 내용이다. 상대성이론만큼이나 그 의미가 큰 이론이며, 양자역학/양자장론의 핵심 이론이다. 현대 물리학에서 대칭의 이해는 그 무엇보다도 중요하다.
만약 그 대칭성이 공간의 한 지점, 지점마다 별도로 적용될 수 있다면, 즉 한 점마다 회전의 각도를 독립적으로 설정할 수 있다면 그것을 국부 대칭(local symmetry) 성이라고 한다. 지역 대칭성은 우리가 현재 기술하고 있는 물리 이론에 불필요한 자유도가 존재한다는 것을 의미한다. 즉, 필요이상의 변수들이 존재하는 것이다. 이것들을 정리하는 과정에서 자연에 내재된 힘, 게이지 입자들이 등장한다.
에미 뇌터의 대칭성 이론, 게이지 대칭성을 제대로 이해하는 것은, 물리학 전공자들에게도 쉽지 않다. 아래는 수학적으로 그 내용을 간단히 설명한 것이다.
=========================
1. 먼저 밴드에 10차례 이상 소개된 action에 대한 정의에서 시작한다. Lagrangian을 이동경로에 따라 (양자장론에서는 공간에 대해서 Lagrangian density 를 전체 공간에 대해) 적분한 값이다. Hamiltonian을 사용해서 정의하는 것도 물론 가능하다. 아래는 좌표 변수 q로 설명한다.

2. 만약 좌표 변환에 대해서 action값이 불변이면 이것을 symmetry transform이라고 부른다. 즉
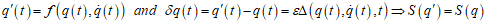
3. 만약 symmetry transform 이 2개 주어지면, 그 둘을 차례차례 적용해도 action 값은 불변이므로 symmetry transform은 group 구조를 띄고 이것을 symmetry group이라고 부른다. 즉,

4. 때로는 이 조건을 좀 더 완화하여, 두 action이 경로가 아니라 두 끝점의 함수만에 의존하는 경우도 허용된다. 즉, 다음 경우에도 symmetry transform이라고 부른다.

5. Symmetry transform에 따른 Action의 변화를 따라가보면

첫번째 적분이 사라진 이유는 Euler-Lagrangian 방정식 즉 EOM(equation of motion)의 경로로 이동했기 때문이다. 위의 식에서 보듯이 symmetry transform에 대해서 action의 변화량이 0이기 위해서는 Q라는 양이 시간에 따라 변하지 않아야한다. 이것의 Noether theorem의 내용이다. 즉, (전역) 대칭에는 보존되는 물리량 Q가 존재한다.
6. 때로는 Q가 0이 아니라 어떤 상수값이 되는 경우로 확장할 수 있다. 이 경우 Noether charge는
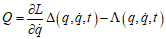
Action의 변화가 0인 것은 다른 말로는 Lagrangian의 변화량이 0인 경우로 생각할 수 있기에 위의 과정을 symmetry transform에 대해서 Lagrangian의 변화가 0이라는 정의로부터도 유도가 가능하다. 즉

이것은 고전 혹은 양자 역학 모두에 대해서 성립하는 양이다. 공간 이동에 대해서 (space translation) 대칭은운동량을, 시간 이동에 대해서 대칭은 (time translation symmetry) 에너지를, 회전에 대한 대칭(rotational symmetry)는 각운동량을, 위상에 대한 대칭성은 전하를 보존한다.
'양자이론' 카테고리의 다른 글
| 통계역학-Ensemble에 대해 (0) | 2021.02.11 |
|---|---|
| 볼츠만 분포 (0) | 2021.02.10 |
| 통계역학 - 맥스웰 분포 (0) | 2021.02.09 |
| 양자역학의 태동 - 아인슈타인의 고체 비열 이론 (0) | 2021.02.01 |
| 양자 역학의 태동 1- 흑체 복사 (0) | 2021.01.29 |




