자신을 인식하는 물질, 존재와 의식... 자연철학적 접근
위상 수학 본문
요즘, 물리학 보다 수학공부에 빠져 있다. 나의 포트 폴리오에 수학 과목이 정식으로 추가되었다. 솔직히 얘기하면 이미, 수학 분야는 수학 학부생보다는 대학원 석사 수준에 가까울 것이고 이제 박사 과정 수준의 수학을 조금씩 맛보고 있다. 밴친이 올린 Millennium problem 문제를 하나하나 쫓아가 보면, 대부분은 현대 수학의 정수에 다다른다. 그것들은, 위상 수학(topology), 미분기하학 (differential geometry), 대수 기하학 (algebraic geometry), 추상대수학(abstract algebra)들이다.
수학에 대한 진입장벽은 무진장 높은 편이다. 그만큼 수학은 명증성이 중요하고, 언어의 통일이 엄격하다. 기초부터 그 용어와 개념들에 익숙하지 않으면 조금만 수준이 올라가도 다른 과목들의 이해는 불가능하다. 다른 모든 체계적인 학문들도 그렇겠지만 수학은 그 정도가 심하다. 때로는, 내가 수학자들의 말장난에 놀아나는 것이 아닌가라는 착각에도 빠진다.
철학은 그 정 반대이다. 각 철학자들은 각자의 무한대의 자유도를 누린다. 그들은 자신들만의 단어를 사용하고, 자신들만의 맥락에서 자신들 독자적인 해석 방법으로 타 철학자들의 생각을 인용한다. 그렇기 때문에, 철학은 엄밀학이 되지 못하였고, 철학적 명증성은, 바로 옆의 철학자를 만나면 바로 무너진다. 물론, 논리 실증주의를 제외하고 말이다. 논리실증주의는 철학보다는 수학에 가까우며, 수리 철학이라고 하여 수학의 명증성에 도전하기도 한다.
요즘 내가 즐겨보는 책은 아래 링크에 있는 Topology와 Physics를 결합한 책이다. 이 책에는 물리학과 수학에 대한 다양한 내용이 있으며, 그 내용은 보통의 물리학 석사 과정 학생도 이해를 못할 정도로 어렵다. 입자 물리학을 전공하려는 대학원생들에게 권하는 책이며, 이 책을 모두 이해하면, 아마 에드워드 위튼이 "Yang Mills mass gap conjecture"을 직접 설명하는 동영상의 이해가 가능할 것이다. 올 겨울에 마스터 하면, 내년 상반기에는 초싸이언으로 거듭나지 않을까 상상한다.
http://staff.ustc.edu.cn/~hyx/0911/(GradMikio%20Nakahara-Geometry,%20topology,%20and%20physics-Institute%20of%20Physics%20Publishing.pdf
==============================
순서를 훌쩍 뛰어넘어, 호지(William vallance Douglas hodge, 1903-1975)라는 영국 수학자에 대해서 간단히 알아보자. 원래 미분기하학에서 자주 접한 이름이지만, 밴친 중 한 분이 Hodge conjecture라는 Millennium problem에 대해서 글을 올려서, 그의 주 전공인 위상 수학 (topology)에 대해서 잠시 사냥을 하고 있기 때문이다. 위상 수학을 공부하시고 싶다면.. 지금 당장 포기하라고 권고한다. 쉽지 않다. 그래도 마음속에서 끓어오르는 앎에 대한 욕구가 있다면, 긴 여정을 떠날 준비를 하시고 길을 떠나시기 바란다.
Hodge는 1903년 스코틀랜드 에딘버러에서 공부 한 후 캠브리지에서 1970년 사망한다. Hodge 추측은 1950년 세계 수학자 대회에서 발표된다. 수학이나 물리학에 관심이 있는 극소수를 제외하고는 평생에 그의 이름을 들어볼 일은 없다. 그의 큰 업적은 미분기하학 (differential geometry)와 대수기하학(algebraic geometry)사이의 관계를 깊이있게 연구한 것이다.
Hodge 추측을 이해하려면 미분기하학과 대수기하학, 위상 수학을 이해해야 한다. 미분 기하학은, 휘어진 곡면위에 존재하는 선의 거리, 곡면위의 두 지점간의 미분, 적분 등의 연산을 하는, 즉, 한 점의 주변에 관한 local 이론(differential)이며 대수기하학은 전역적인 (global)한 도형의 모양을 결정하는 기하학(geometry)이고 호지 추측은 이 둘을\ 결합하는 방식에 관한 수학이론이다. 미분기하학을 이해하면, 아인슈타인의 일반 상대성이론은 1시간 이내에 이해가 가능하다. 다른말로는 아인슈타인은 에너지로 인한 공간의 휘어짐이라는 기본 아이디어를 구상 후, 10년 동안 친구 수학자 그로스만의 도움으로 리만 기하학을 공부한다.
이제, Hodge conjecture, 호지 추측 문제를 기술해 보자. 먼저 영어로는,
“Let X be a non-singular complex projective manifold. Then every Hodge class on X is a linear combination with rational coefficients of the cohomology classes of complex subvarieties of X.”
영어라서 어려운 것이라 판단하고 한글로 번역하면
“특이하지 않은 투사 대수 다양체 상에 있는 임의의 조화 미분 형식은 대수 사이클들로 이루어진 코호몰로지 집합들의 유리 조합이다."
한글이 더 어렵다. 문제라도 정확히 이해하려면, 위상수학과 미분기하학을 이해해야 한다. 내용 자체가 그렇게 어려운 것은 아니다. 그러나 그것을 이해하고 설명하려면 그 두 언어를 익혀야 한다. 새로운 언어를 익히는 것은 한편으로는 재미있고, 한편으로는 고통스럽다. 특히, 나이가 들면 들수록 기존 지식들이 새로운 지식의 진입을 방해한다.
호지 추측을 간단히 얘기하면, 우리가 local rule 을 지키면서 (즉, 미분 형식을 유지하면서) 인간의 뇌로는 그릴 수 없는 일반적인 다차원 공간에 그린 도형들은 global rule을 따르는 대수 기하학적인 도형들의 유리수 결합으로 만들 수 있다는 얘기이다. 즉, 진짜 이상하고 특이하게 그리지 않는 한, 대부분의 우리가 그릴 수 있는 도형들은 방정식의 형태로 표시할 수 있다는 간단한 의미이다.
현재 Hodge conjecture은 그 진위 여부도 명확하지 않고, 증명도 이루어지지 않은 상태이다. 잘 알다시피, 각 문제당 100만불이 걸린 millennium problem 7개 중, 푸앙카레 추측을 제외하고는 한 문제도 풀리지 않은 상태이다. Hodge conjecture에 위배되는 반증사례 하나만 만들 수 있다면 힘들게 증명하려고 노력하지 않아도 간단히 100만불을 받을 수 있다. 그리고 그 순간, Hodge conjecture를 가정한 많은 논문들은 바로 쓰레기 통으로 직행할 것이다.
==============================
위상 수학은, 주어진 공간의 구멍의 수를 세는 homology와, 주어진 공간을 연속적으로 변형하는 homotope로 구성된다. 위상수학은 흔히 푸앙카레(1854-1912) 가 만들었다고 얘기한다. 푸앙카레의 추측은 아주 간단한 얘기를 증명하라는 얘기이다. 푸앙카레는 프랑스의 대수학자이며 물리학과 수학의 다방면에서 거대한 업적을 남긴다. 과학계에서 그를 “the last universalist”라고 부르기도 한다. 수학에 큰 관심이 없어도 푸앙카레 추측, 페렐만의 얘기로 많은 이들이 그의 이름을 익히 알고 있다.
그의 가장 큰 공헌은 위상수학(topology)라는 새로운 수학 분야를 개척한 것이며, 위상 수학과 대수기하학의 깊이있는 이해에 큰 기여를 하였고, 아인슈타인보다 먼저 특수 상대성이론의 기본 골격을 완성한다. 또한 수리/과학 철학에도 기여를 하여 논리 실증주의의 기반을 마련하는데도 영향을 준다.
그는 1854년 프랑스 로렌주의 낭시에서 출생하고, 어렸을 때부터 신동으로 이름을 날린다. 에콜 폴리테크니크 수석입학/차석졸업(수석은 누군지 궁금 ^^)한다. 프랑스 고교졸업시험인 바칼로레아에 낙제하였으나 그것은 프로에센 프랑스 전쟁이 그가 살던 알자서-로렌주에서 터졌기 때문이라고 한다. 그 이후로 쭈욱 정석적인 생활, 모범생 생활을 했기 때문에 특이한 일화가 많지는 않고, 드레퓌스 사건에서 진보진영에서 드레퓌스의 무죄를 적극 주장한다.
푸앙카레 가설은 클레이 수학연구소의 Millenium 7대 문제 중, 문제 자체는 가장 간단히 설명할 수 있다. 한마디로 얘기하면 “공처럼 생긴 것은 공이며, 공의 형태로 만들 수 있다 ^^”. 이 말을 듣고 “Duck test”를 떠올릴 분들도 있을 것이다. “If it looks like a duck, swims like a duck, and quacks like a duck then it probably is a duck” “오리처럼 생기고, 수영하고 짖으면 그것을 바로 오리라고 부른다”
물론, 전문적인 수학용어로는 아래와 같이 조금 fancy하다.
“모든 경계가 없는 단일 연결 콤팩트 3차원 다양체는 3차원 구면과 위상동형이다” (Every simply connected, closed 3-manifold is homeomorphic to the 3-sphere)
간단히 얘기하면 다면체와 다면체들의 연결은 적당히 찌그러뜨리면 구의 형태로 만들수 있다는 얘기이다. 이 간단한 내용의 증명에 100여년이 걸렸으며, 그 해결에 결정적인 힌트는 사실 페렐만이 아니라 Richard Streit Hamilton(1943-)이라는 현 콜롬비아 대학 수학과 교수가 제공하였다.
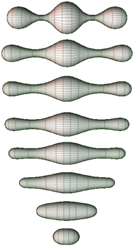
그 방법론은 Ricci flow라는 방법이다. Ricci는 물리학을 공부하는 사람들에게는 너무나 유명한, 낯익은 이름이다. Einstein 의 장방정식(field equation)의 한 항이 Ricci scala항을 포함하고 있기 때문이다. Riemann, Ricci tensor를 모르고 Einstein의 일반상대성이론을 얘기할 수는 없다. Ricci flow는 열확산 방정식과 형태가 아주 유사한 간단한 미분 방정식을 말한다.

Ricci flow는, 특정한 다양체 (manifold)의 metric tensor가 주어진 경우, 시간에 따라 metric tensor가 어떻게 진화해 나가는지를 계산한다. 기본적으로 Ricci flow는 열확산 방정식과 동일한 형태이다. 공간에서 한 쪽의 온도가 높고, 다른쪽이 낮으면 온도가 높은 쪽에서 낮은 쪽으로 퍼져 나가서 엔트로피가 최대화되는, 즉 균일한 공간으로 확산된다. 공간에 대해서 이를 적용해 보자.
공간이 물렁공이라고 생각해 보자. 처음에 모양은 구겨져 있을 것이다. 그러나, 어떤 한 점의 주변을 살펴보면 일정한 곡면으로 근사화할 수 있고 자체 곡률을 가질 것이다. 여기에 Ricci flow를 적용하여, 그 공간을 변형시켜 보자. Ricci flow의 역할은 공간을 부드럽게 변형시켜서 결국은 시간이 지나서 다시 동그란 모양으로 변하는 것을 목적으로 한다.
수학자 해밀턴은 이 간단한 Ricci flow가 푸앙카레 문제를 해결할 수 있는 마스터 키임을 수학계에 발표하고 본인 자신이 푸앙카레 가설 해결에 도전한다. 그러나, 어떤 경우에는 공간이 점점 더 sharp 하게 변해서 특이점을 생성하는 경우가 발생한다. 예를 들어, 원추형 꼴의 꼭지점을 생각해 보자. 이 부분은 아무리 공간을 확장해도 여전히 뾰족한 형태에 머문다. 이러한 점을 특이점(이경우에는 conic singularity)이 존재한다고 얘기한다.
우리는 그러한 가늘고 긴 뾰족점을 구부리면 동그랗게 변함을 안다. 그러나 그 부분은 아무리 시간이 지나도 영원히 그러한 모양으로 남으므로 원의 형태로 구부려지지 않으므로 Ricci flow 방법으로는 원의 형태로 만들 수 없다. 따라서, 해밀턴은 Scissor로 그 끝부분을 싹둑 잘라서, 동그란 모양의 마개를 꽂는 방법을 고안한다. 동그란 부분은 시간이 지나면 편평하게 곡률이 일정한 곡면으로 변형되기 때문이다.

그러나 문제는, 그러한 뾰족점이 유한 개가 존재하여, 이렇게 자르는 과정이 finite time에 끝날 수 있느냐는 문제와 그러한 뾰족점이 단순히 원기둥 모양으로 변하여 요렇게 잘라내는 것으로 간단히 문제가 해결될 수 있느냐는 것이다. 해밀턴은 이 부분에서 막혀서 더 이상 진도를 나가지 못한다. Parelman은 해밀턴이 막힌 부분을 집요하게 연구하여 모든 특이점들은 원통형이며 그들의 개수도 유한 개임을 보임으로써 푸앙카레 가설을 증명한다.
수학자들은 푸앙카레 가설이 수학적인 문제라고 생각했지만, 패렐만은 이 문제에 물리학적인 직관, 즉, 엔트로피의 개념을 도입한다. 그의 논문이 처음에 Arxiv라는 정식 논문지가 아닌, 인터넷 사이트에 올라왔을 때, 사람들은 이게 모지.. 하는 반응을 보였다.
요즘, 페르마 정리, 푸앙카레 추측, 호지 추측, 양밀스 질량 간극 가설 등 여러 수학적 난제들을 살펴보고 있고, 그 해결의 history를 쫓아가 보고 있다. 그러면서 느끼는 것은 세상에 참으로 많은 천재들(돌연변이들)이 있고, 다른 한편으로는 세상에 설명되지 못할, 충족이유율을 만족하지 못하는 천재는 한명도 없다는 사실을 느낀다.
'수학사' 카테고리의 다른 글
| 푸앙카레, 위상수학 (0) | 2021.09.27 |
|---|---|
| 천, 사이몬스 (0) | 2021.02.04 |
| 해밀토니언, 해밀턴 역학 (0) | 2021.02.03 |
| 복소함수 해석학, 코쉬 (0) | 2021.02.03 |
| 라그랑지 (0) | 2021.02.02 |




