자신을 인식하는 물질, 존재와 의식... 자연철학적 접근
Ising model, 이징 모델 본문
#물리학#통계역학
오늘 게시글은 Ising 모델에 관한 내용인데, 수식으로 시작해서 수식으로 끝나므로 아무도 쫓아오지 못할 것이다. 그래서 다른 얘기들, 사족들을 조금 붙인다. Ising model이라는 통계역학에서는 유명한 얘기지만, 일반인들은 전혀 모르고 있는 내용에 관한 배경 설명이다.
왜 물은 정확히 100도에서 급격하게 상변이를 하고 왜 374도에서 액체 상태는 갑자기 흔적도 없이 사라지는가? 왜 자석은 퀴리온도를 넘으면 자석의 성질을 잃어버리고 그것보다 조금만 낮으면 자화가 가능한가?
물리학에서 문제에 접근하는 방법은 대개는 미분을 사용한다. 미분의 철학은, 만약 시간 간격이 작다면 두 물리 현상 간에는 선형적인 관계에 있다는 것이다. 우리가 급격하게 방향을 바꿀때에도 짧은 구간구간으로 분해하면 우리는 예측 가능한 움직임을 하고 있다. 즉, 현재의 시간과 현재의 속도로 부터 앞으로 10초후의 일을 예측하지는 못하지만 0.001초 후의 일은 거의 오차 없이 예측할 수 있다. 그러나, 이렇게 0.1도만 차이나도 확 변해 버리는 불연속적인 사건을 해석하는 것은 쉽지 않다.
이러한 비선형적인 문제를 다뤄보기 위해서 독일 Hamburg 대학의 Wilhelm Lenz (1888-1957)는 대학원생 Ising을 잘 교육시켜서 1920년에 불연속적인 위상 천이 과정을 설명할 수 있을 것으로 기대하여, 자석의 자화에 대한 작은 toy model, 아주 단순한 수학적 모델을 만든다. 그 모델은 앞서 설명한데로 아래 수식으로 주어진다. 아래 수식의 의미는 인접 영역의 2 스핀이 동일한 방향으로 정렬되면 에너지가 낮아진다이다.

온도란 무엇인가? 온도는 기체의 운동 에너지이고, 이것은 기체들이 자유를 향해서 제멋대로 행동하게 하는 원동력이다. 만약 외부에서 아무런 제약 조건이 없다면 존재들은 entropy 가 최대로 되는 방향, 존재의 자유도가 가장 높은 방향, 완전히 random하여 아무도 더 이상 어떤 의미있는 예측을 할 수 없는 지점에서 평형 상태를 ㅡ이룬다. 그러나, 위의 제약 조건에 의해서 존재들은 entropy 를 최대화 하려는 힘과, 에너지를 낮추려는 힘 사이에 줄다리기를 한다.

이제 조금있으면 노벨상을.. 흐뭇하게 상상하던 Lenz 교수에게 Ising 이 가져온 답은 처참하게도, 1차원 Ising model에서 상전이 현상은 존재하지 않는다는 것이었고, 2차원 이상은 풀지 못했지만, 개고생해보니.. 그것들도 당연 안될 것 같다고 얘기한다. 같이 얘기를 듣던, Pauli (파일리는 모르는 이는 없을테고)도 덩달아 한숨을 쉰다. 그의 말을 들어보면
“...I discussed the result of my paper widely with Professor Lenz and with
Dr. Wolfgang Pauli, who at that time was teaching in Hamburg. There
was some disappointment that the linear model did not show the expected
ferromagnetic properties...”.
그러나 20년이 지난 1941년, 거의 야스퍼거 증후군 수준의 소통 불능의 대가 Onsager는 그 어려운 2D-Ising 문제를 성공적으로 풀고, 2차원 이상에서는 phase change가 존재함을 증명한다. 그 이후, 통계 역학의 많은 교과서들이 Ising model을 이용하여 상변이를 설명하고 (그 공로로 1968 노벨화학상 수상), 최근까지도 Ising model에 관한 여러 연구 결과들이 발표된다. 여기까지만 읽으면 될 것이다.

<Ising (좌측)과 Pauli (우측)>

=======================================
이전 게시글에서는 Ising problem을 mean field theory를 이용해서 근사적으로 계산하였다. 그러한 근사적인 계산으로도 어느정도 정성적으로 상변이 과정을 파악할 수 있었다. 이번에는 d=1, d=2 인 경우에 Ising problem을 풀어보자. 이미 얘기한데로 d=1인 경우는 Ising이 학위 논문으로 정확히 풀었고, d=2인 경우는 그 수학적 난해함으로 20년 후에 Onsager에 의해서 풀린다. 그 공로로 Onsager는 노벨화학상을 수상한다.
먼저 d=1, 1차원 문제에 대해서 풀어보자. 이 경우는 정확히 계산이 가능하다. 계산을 위해서 먼저 s1은 s2와 s2는 s3와 … 이렇게 연결되고 sN은 s1으로 다시 연결된다고, 즉 주기적이라고 가정하자. 어차피 N은 아주 큰 값이기에 boundary 가 전체에 주는 영향은 적을 것이고, 경계를 넘어간 영역에는 우리의 관심이 적기에, 이러한 가정은 reasonable한 가정이다.

보통 행렬 T의 N지수승을 구하려면, 그 방법은 eigen decomposition, 즉, eigen space에서 대각화를 수행하는 방법이다. 선형 대수학을 배운 이들은 내가 지금 하고 있는 말을 이해할 것이고, 그렇지 않은 이들에게는 의미없는 얘기일 뿐이다. 그러나, 구글링을 해보면 그 개념은 금방 catch할 수 있다. 어떤 행렬의 trace는 eigen value들의 합과 동일하다는 것을 선형대수학에서 배우고, 이를 이용하면 아래와 같이 partition function을 정확히 구할 수 있다. 그리고, 마지막에 보인 바와 같이, 1차원 Ising problem에서는 magnetization m은 항상 0이다. 즉, 1차원구조의 자석은 존재할 수가 없다. Entropy force가 energy force에 대해서 항상 승리한다. Thermal fluctuation 때문에, 조그만 자석들이 한방향으로 절대로 정렬이 안된다는 얘기다. 이것은 mean field theory에서 예측한 결과와는 정반대이다.

D=2인 경우에는 정확히 계산하는 것이 쉽지 않다. 따라서, 이 경우에는 온도가 아주 높거나, 온도가 아주 낮거나 하는 두가지 경우에 대해서만 근사적으로 해를 구해 본다.
1. 먼저 B=0이고 첫번째 경우로 온도가 낮은 경우 (T가 작고, 따라서 beta가 큰 경우)에 partition function은 saddle point approximation 에 의해서 가장 에너지가 낮은 상태 혹은 그 주변에 의해서 Z값이 결정된다.

가장 에너지가 낮은 상태는 아래 그림에서 보듯이 모두가 하나의 spin으로 정렬된 때이다. 이때 sisj=1이고 에너지 E0=-2NJ 이다 (2차원이기에 d=2이고, 한 개의 격자점 당 4개의 nearest neighbor가 있지만 중복을 제외하면 2N개의 {ij}쌍들이 존재하기 때문이다).

그 다음으로 에너지가 낮은 상태는 1개 격자점의 spin 만 반전된 경우이고 아래 그림과 같은 경우이다. 이 경우의 에너지는 E1=E0-8J임은 쉽게 알 수 있다. 그리고 동일한 에너지 E1에 대해서 N개의 가능성이 (격자점 하나마다 하나씩) 존재함을, 즉 degeneracy=N임을 알 수 있다.

그 다음은 6개의 bond가 깨어진 경우, 즉 아래 그림과 같은 경우이다. 이 경우 에너지는 E2=E0-12J 이고 가로 혹은 세로 방향의 연속점들을 선택할 수 있기에 이 경우에는 degeneracy=2N이다.

마지막으로 8개의 bond가 깨어진 경우는 다양한 조합이 가능하다. 각각을 모두 설명할 필요는 없고 그림을 잘 살펴보면 각각의 경우에 가능한 조합의 수인 degeneracy를 쉽게 파악할 수 있다. 아래에서 제일 위에 있는 경우는 2개의 서로 떨어진 graph의 경우에 해당하는 데, 양자장론의 경로 적분법에서 종종 만나듯이 이렇게 떨어져 존재하는 graph는 다른 항들에 의해서 상쇄되어 최종 결과에서는 사라지게 된다.

이제까지의 계산 결과들을 종합해서 partition function을 근사적으로 구해보면, 아래에서 보듯이 N^2 항, 즉, disconnected graph 에서 기인하는 항들은 사라진다. 나중에 양자장론을 공부하면 이러한 경우를 자주 만나게 된다.

2. 이제 반대로 온도가 높은 경우 (B=0, T>>1, beta<<1)에 대해서 partition function이 어떻게 전개되는지 살펴보자. 먼저, 가장 dominant 항은, 모두가 random할 때, 즉, entropy 가 최대일 때로 아래와 같이 전개가 된다.

이제 다음항을 살펴보면 다음과 같이 closed loop 이 아닌 모든 경우에 대해서 합은 0이다.

그렇지 않은 경우는 아래 그림과 같이 closed loop을 이루는 경우이고, 이러한 모든 closed loop에 대해서 계산하면 Z를 모두 계산할 수 있다. 가장 작은 loop은 아래 그림과 같이 4개의 point로 구성되는 경우이고 1번 꼭지점은 2D lattice의 어떤 점이든 가능하므로 degeneracy는 N이다.

그 다음 경우는 아래와 같이 6개의 point로 이루어진 경우이며 그것은 가로 혹은 세로로 긴 경우를 고려할 수 있으므로 degeneracy는 2N이다.

그 다음은 길이가 8인 경우이고, 이 경우에는 4가지 종류가 가능하다. 그 중 한가지는 2 loop 이 disconnected된 경우이고, 나머지는 모두 단일 loop의 경우이다.
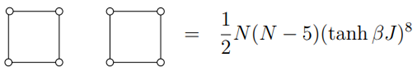



이제까지의 항들을 고려하여 partition function을 구해 보면 아래와 같다. 그런데, 아래 식은 웬지 너무 낯익다. 왜냐하면 바로 좀 전에, 저 위에 온도가 낮은 경우에 만난 경우와 형태적으로 거의 동일하기 때문이다. 즉, low temperature expansion 식에 sinh 를 1/sinh으로 대체하면 2개의 이론은 동일하며 이것을 Kramers-Wannier duality라고 부른다. 물리학을 공부하다 보면, 하나의 이론이 다른 이론과 형태적으로 동일한 경우를 자주 본다. 만약 초끈 이론을 배운다면 Ads-CFT이론이라는 것을 접하게 된다. 지난 20여년간 입자 물리학의 연구 결과중 가장 중요한 이론으로 Maldacena가 1997년에 발표한 이론인데, 비슷한 얘기를 하고 있다.

'양자이론' 카테고리의 다른 글
| 디락 방정식 II (0) | 2021.04.16 |
|---|---|
| 자연은 왼손잡이 (0) | 2021.04.15 |
| 자화와 상전이 현상 (0) | 2021.03.06 |
| 이징 모델, Ising model (0) | 2021.03.05 |
| 물질의 상변이, phase transition (1) | 2021.03.04 |




