자신을 인식하는 물질, 존재와 의식... 자연철학적 접근
전자 축퇴압 본문
샌프란시스코 근처에 Half moon bay 란 곳이 있다. 태평양을 바라보는 절벽 위에 리츠 칼튼 호텔이 있고, 태평양을 바라보면서, 태평양을 넘겨서 칠 수 있는 골프장이 있다. 그냥 지나가는 길에 구경삼아 들른 곳인데, 은퇴 후에 꼭 다시 들러보고 싶은 곳 중 한 곳이다. 그때까지 건강해야 할 텐데, 요즘은 매년 내 몸에서 흥미로운 현상들이 나타나는 듯 하다. 작년 한해는 후두염으로 고생했는데, 올해는 내 몸에 어떤 것이 다가올 건지 자못 기대된다 ^^.

=============================
인간들은 직관의 힘을 너무 과신한다. 직관적으로 이해가 되면 본인은 깨달았다고 생각한다. 그러나 대부분의 경우에, 직관은 감정이나 느낌에 의존한다. 감정이나 느낌은 편도체가 관여하며 전두엽의 힘은 약하다. 그러한 느낌은, 본질적인 질문을 만나면 한 순간에 무너진다. 논리적 토대가 약하기 때문이다. 수학적 기반위에서 튼튼히 쌓아올린 개념은 그러한 질문에도 잘 무너지지 않는다.
우리가 동전을 아무리 눌러도 동전은 꿈쩍도 하지 않는다. 그 조그만 동전은 어떻게 우리의 힘을 견뎌내는 것일까? 동전은 금속이다. 앞서의 질문에 대답을 하려면 금속의 성질을 수식적으로 따라가봐야 할 것이다. 금속은 원자들이 결정 형태로 나열된 것이다. 대부분 어느 정도 무거운 원소들의 배열로 구성된다. (하지만 스티로폴보다 100배나 가벼운 금속도 존재한다) 원자수가 높은 원자들의 경우, 최외곽 전자들을 붙들어 두는 힘이 약하기 때문에, 그들은 한 원자에 귀속하지 않고 결정내를 떠돌아다니고 이를 자유 전자라고 부른다.
전자는 spin수 1/2인 Fermion 입자이다. 따라서, 이전에 얘기한 3가지 통계중, Fermi-Dirac 통계를 따른다. 전자의 Grand partition function 과 grand free energy, 그리고 어떤 에너지 대역에 전자가 존재할 확률은 아래 세개의 수식으로 나타난다. 아래 그림에서 보듯이, 온도가 낮으면(T->0) Fermi level 이라고 부르는 chemical potential energy 밑으로는 모두 점유되고 그 이상은 완전히 비어 있게 되고, 온도가 올라가면 Fermi level 주위로 점점 더 넓게 분포한다.


Fermion 들은 두 입자를 교환하면 파동함수가 사라진다. 따라서, 두 개의 Fermion은 동일한 양자 상태, 만약 양자 상태가 에너지 레벨에만 의존한다면, 동일한 에너지 레벨에 절대 공존할 수가 없다. 이것을 Pauli의 배타원리, exclusion principle라고 부른다는 것은 이미 귀가 따갑게 들었을 것이다. 따라서, ground state부터, 차곡차곡 전자들을 쌓아서 일정 에너지 대역까지 전자들이 쌓이게 된다. 이것을 정량적으로 계산해 보자.
계산을 위해서 LxLxL 크기의 box에 전자가 갖혀있다고 가정하자. Bounded state에서 전자의 파동함수는 경계 조건을 만족해야 하기에 가질 수 있는 wave number k값이 (따라서 에너지가) 양자화된다. 이제, 흑체 복사, 혹은 boson의 상태 수를 계산하는 과정등 여러 과정에서 사용한 기법(k 혹은 n 공간의 점의 개수를 세는 문제를 적분으로 근사화하는 방법)을 적용하면 아래와 같이 density of state, 즉 특정한 에너지 대역 E에 존재하는 양자 상태의 밀도를 구할 수 있다. 아래 수식의 결론은, 에너지가 증가할수록 상태 공간이 root(E)에 비례해서 증가한다는 사실이다.

이제 온도를 아주 낮추어 T가 0도에 근접할 때에, 점유 가능한 양자 상태가 몇 개인지를 계산해 보자.
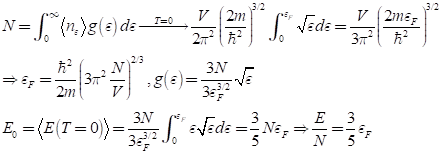
위의 계산들이 재미가 없을지 모른다. 그렇지만 그 의미는 심오하다. 별들의 내부에서 모든 연료들을 다 태우고 나면, 더 이상 태울 재료가 사라지면 온도가 서서히 내려가고 절대 온도 0도에 이른다. 절대 온도 0도에서 존재들은 더 이상 움직일 수 있는 힘이 사라지므로, 고전 역학적인 운동에너지는 0이 되고, 이제 중력에 대항할 힘은 모두 사라진다. 그러면, 존재들은 중앙을 향해서 끊임없이 낙하를 하고, 특이점에 도달할 것이다. 그러나, 모든 별들이 블랙홀이 되지 않는다. 왜 그런가? 어떤 힘들이 그 낙하를 저지하는가? 위에서 구한 수식 때문이다. 이것을 전자 축퇴압, electron degeneracy pressure라고 부른다.

위의 식들이 에너지로 나타나 있어, 압력과의 관계가 어리둥절할 수도 있다. 압력은 단위 면적당 누르는 힘으로 계산할 수도 있고, 부피의 변화에 따라 에너지의 변화량으로 구할 수도 있다. 즉, 아래와 같은 압력이 중력이 Fermion을 끌어당겨서 압축하려고 할 때, 이에 대항하는 힘, 절대 온도 0에서도 나타나는 양자역학적인 축퇴압이고, 이 때문에 백색 왜성은 에너지를 모두 소모한 뒤에도 그 형체를 오랫동안 유지하게 된다.

왜 동전을 눌러도 찌그러지지 않는가? 동전을 누르는 힘에 반발하는, 현재의 영역을 고수하려는 전자들의 강한 압력, 파울리의 배타원리에 의한 전자 축퇴압이 이를 저지하기 때문이다.

'천문학' 카테고리의 다른 글
| 블랙홀, 펜로우즈 도형 (0) | 2021.04.17 |
|---|---|
| 블랙홀 단상 (0) | 2021.04.17 |
| 블랙홀 단상 (0) | 2021.04.10 |
| 블랙홀 (0) | 2021.04.10 |
| 우주 방정식 - 프리드먼 방정식 3 (1) | 2021.04.09 |


