블랙홀, 펜로우즈 도형

 

블랙홀자료를 보다보면 Penrose diagram(펜다)을 가끔씩 볼 때가 있습니다.

펜다는 무한대의 시공간을 유한한 시공간으로 표시하기에 우주 규모의 시간대에서 이루어지는 운동의 궤적을 개념적으로 쉽게 이해할 수 있게 표현해 줍니다. 펜다는 어떻게, 어떤 원리로 구성된 것일까요? 수식을 통해서 정리해 봅니다. 먼저, 민코프스키 공간을 극좌표계로 표시합니다.

 

위 공간을 그냥 종이에 그리자면, t와 r이 각각 -무한대 ~무한대,0~무한대의 공간이므로 아주 큰 종이가 필요하겠죠? 따라서 좌표 변환을 해야 합니다. 먼저 (t,r)좌표계를 (u,v)좌표계로 아래와 같이 변환합니다. 복잡해 보이지만 그냥 (t,r)축을 45도 회전시킨 것에 불과합니다.

 

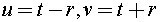
물리학자들은 흔히 광속이나 플랑크 상수를 1로 두고, 나중에 값을 대입하기를 좋아하죠. 위의 변환도 마찬가지로 광속 c=1로 둔 경우입니다. 빛이 원점에서 출발하였다면 r=ct=t로 표시되겠죠? 따라서 u=t-r=0는 원점으로부터 시작한 빛의 궤적을, v=t+r=0은 원점에 도달하고 있는 빛의 궤적을 나타냅니다. 이것을 null-coordinate라고 합니다. 즉, (u,v)에서 u와 v축은 각각 원점에서 멀어지는(도달하는) 빛의 경로를 나타내는 null-coordinate입니다. 이 좌표계에서 minkowski metric은 다음과 같이 표현됩니다.

 

여전히 아주 큰 종이가 필요하죠? 따라서, 공간을 압축하는 비선형 변환을 수행합니다. tan(a)는 a가 -pi/2~pi/2까지 변하면, 그 값이 -무한대~무한대의 값을 가집니다. 따라서 역함수인 atan()을 취하면 반대로 무한의 세계를 한정된 공간으로 변환할 수 있습니다.

 

(U,V)좌표계에서의 conformal metric은 아래와 같이 주어집니다..

 

이제까지 한 일은 conformal null coordinate를 만든 것이죠. 즉, 빛의 이동경로를 축으로 하는 null coordinate를 설정하고 (따라서 모든 시공간에서 light cone은 일정한 각도의 깔때기 모양으로 표시되고, 따라서 두 지점 간의 causal relationship 파악이 쉬워졌죠), 종이에 우주 전체를 그릴수 있게 -무한대~무한대의 길이를 -pi/2~pi/2의 공간으로 압축한 것입니다.

이제 위의 축을 다시 반대방향으로 45도 회전시키면 원래의 t,r 축을 회복할 수 있겠죠. 이를 위하여 T,R축을 도입하는데 (T,R)=(U+V, U-V)로 원래 방향으로 회전시킵니다. 이렇게 변환된 최종 좌표계에서의 metric은 다음과 같습니다.  

 

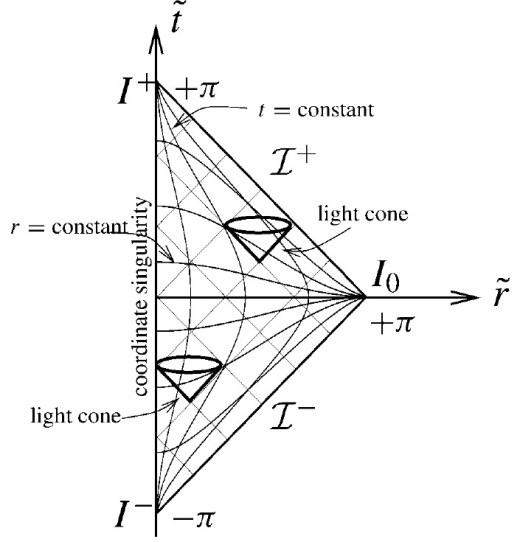
이것을 그림으로 나타내면 아래와 같은 최종 penrose diagram이 얻어집니다. 아래 그림에서 I0는 space infinity, I-는 past timelike infinity (최초), I+는 future timelike infinity(최후) 이고 45도 직선에 해당하는 I-,I+는 각각 past null infinity (빛의 시점), future null infinity(빛의 종점)라고 불리는 면입니다(원래는 원뿔 혹은 hyperspace모양의 입체임을 유념).  Penrose diagram에서 입자들은 light cone 방향으로 운동이 가능합니다.