자신을 인식하는 물질, 존재와 의식... 자연철학적 접근
겔만, 팔정도 본문
겔만의 eightfold way를 분석하다 보면 아래의 Gelman nishijima공식을 만나게 된다. Q=I+Y/2라는 아주 간단한 공식이다. 1953에 Nishijima라는 일본인 물리학자가 먼저 제안하고 이와 독립적으로 겔만이 1956에 발표한 공식이다. 왜 Iso-spin과 Hyper charge가 electrical charge와 이렇게 관계를 맺어야 할까? 어쨌던, 아래 공식이 왜 성립하는지는 모르겠지만, 양자수들로부터 아래 공식이 성립함을 이해하는 것은 1분이면 될 정도로 간단한 공식이다.

이전 포스팅에서 올린 마지막 그림을 보자. Up, down, strange quark의 양자수를 기술한 그림이다. 가로축이 Isospin, 세로축이 Hypercharge를 의미한다. 이전 포스팅에서 얘기한데로 I+, U+, V+에 의해서 입자들은 모습을 바꾼다. 화살표의 방향을 보면 I+는 d를 u로 변환하는 연산자임을 알 수 있다. ladder operator라고 부른다. U, d, s입자란 SU(3)를 표현하기 위한 힐버트 공간에서 세가지 가능한 state의 일종이다.

up quark = (I3,Y)=(1/2,1/3)의 값을 가진다. 따라서 electrical charge = 1/3+1/6=2/3을 가진다. 아래 표의 내용과 일치한다. 나머지 입자들에 대해서도 연습해 보시기 바란다.

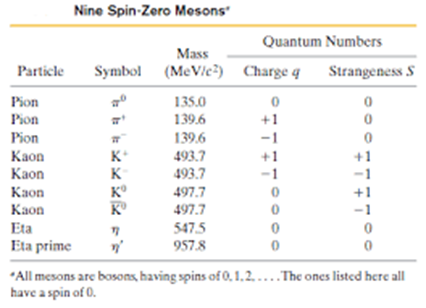
이제 meson(중간자)를 나타내는 8정도의 하나를 살펴보자. Meson은 quark와 anti-quark로 구성된 입자이다. 그 반면 baryon은 3개의 quark로 구성된다. 아래 그림을 보다면 대각선으로 비스듬하게 줄이 쳐진 선이 electrical charge를 나타내는 선이다. 아래의 그림을 보고 Gelman Nishijima의 공식을 떠올려야 한다.

위의 그림을 보고 다시 아래와 같은 meson 입자의 quantum number에 관한 공식을 이해하면, 군이론적인 원리는 모르더라도 8정도의 형태적인 요소는 이해한 것이다. 그러나 meson과 baryon의 다양한 모습들이 SU(3) 군이론상에서 상태 공간에 나타날 수 있는 모든 모습이라고 이해할 수 있다면, 즉, particle이 SU(3) group representation이라고 이해하신다면 우주의 본질을 좀 더 정확히 이해한 것이다.
'양자이론' 카테고리의 다른 글
| 겔만, 리대수학과 팔정도 (2) | 2021.04.26 |
|---|---|
| 겔만, 입자들의 규칙 팔정도 (1) | 2021.04.26 |
| 겔만, 입자 동물원을 정리한 팔정도 (0) | 2021.04.24 |
| 디락 방정식 I (0) | 2021.04.16 |
| 디락 방정식 II (0) | 2021.04.16 |




