자신을 인식하는 물질, 존재와 의식... 자연철학적 접근
겔만, 입자들의 규칙 팔정도 본문
8정도, eight fold way는 Gelmann 이 만든 입자 정리도이다. 1960년대, 물리학자들이 궁극의 입자를 찾고자 입자가속기를 돌린다. 그들의 눈에 곧 튀어나올 모든 입자들의 입자를 기대하면서 말이다. 그러나, 웬걸.. 수십종의 걸레 같은 입자들이 계속 나오는 것이 아닌가.. 이거 뭐, 정리도 안되고.. “괜히 사서 고생했다.. 걍 모르고 있을 걸” 아마 속으로 이런 생각을 했을 것이지만, 겔만은 그 가운데서 아주 아름다운 수학적인 규칙을 찾는다. 그것을 겔만은 불교적 용어인 eight-fold way, 8정도로 설명한다. 물론, 불교의 8정도와 관련성은 1도 없다. 아래에 meson 에 관한 그림 한개를 예시로 들었다. 8개의 meson 입자의 규칙성을 설명한 그림이다.

=================================
강력은 SU(3)_c라고 되어 있다. 즉, 아래 첨자로 c가 있다. 그것은 color charge를 의미한다. 입자들을 정리하는 것은 color charge와는 무관한 (u,d,s) 즉, 3가지 종류의 flavour space상의 회전 대칭성에 의해서 주어진다. 그러나 그 둘은 모두 SU(3)공간에서 기술되기에 둘의 묘사는 유사하다. 이번 포스팅에서는 (u,d,s) 공간상의 회전 대칭성에 따라 존재할 수 있는 여러 입자들을 기술해 보자.
Quark, 그 당시에는 세가지 quark를 생각하였다. (u,d,s), up/down/strange quark 이렇게 세 종이다. Flavour 공간에서의 회전 대칭성 SU(3)를 생각하자. u=(1,0,0), d=(0,1,0), s=(0,0,1) 요렇게 묘사된다. SU(3)의 generator는 아래와 같은 8개의 행렬이다. 정확히는 아래 행렬의 반인 T=1/2lambda를 SU(3)의 generator라고 하며 su(3) lie algebra 공간을 생성하는 기저 벡터 (basis vector)들이다.

위의 행렬을 잘 살펴보면 SU(3) 공간에는 3개의 SU(2)가 subalgebra로 존재함을 알 수 있다. 예를 들어 {l1, l2, l3} 의 경우 2x2 행렬을 살펴보면 바로 파울리 행렬 즉 SU(2)공간임을 알 수 있다. 마찬가지로 {l4, l5,(l3+l8)/2}, {l6, l7, (l3-l8)/2}도 SU(2)공간임을 금방 알 수 있다. 그 부분을 이해하면 8정도의 이해에 큰 도움이 된다.
SU(2)이론은 각운동량 연산을 할 때 이미 많이 다루었다. 그 중에 양자수를 하나 올리는 ladder operator (상승, 하강 연산자)를 사용하면 vacuum energy state로부터, 모든 energy state를 생성할 수 있었다. 이것은 SU(3)에도 동일하게 적용이 가능하다. Group의 generator는 Hermitian matrix이다. 그룹 D의 generator중 서로 간에 교환이 가능한 것들을 모두 모으면 그들은 동시에 대각화가 가능하고 이것들을 Cartan generator라고 부른다. 그리고 그 갯수(cartan algebra의 dimension)를 원래 그룹 D의 rank라고 부른다. Su(n)의 경우 rank는 n-1이다. 즉, su(2)의 경우 1개, su(3)의 경우 2개이다. Su(3)의 경우는 위에서 보았듯이, l3, l8의 2개가 cartan generator들이다.
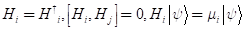
어떤 algebra 중, 모두 동시에 대각화가 가능한 elements만 모아두면 이것을 cartan subalgebra라고 부른다. Cartan subalgebra의 dimension을 원래 algebra g의 rank라고 부른다. Su(n)의 경우 rank는 n-1이다.
양자역학에서 각운동량 연산자를 배울 때에 흔히 casimir(카시미르) operator를 얘기한다. (x,y,z)축 방향의 각운동량 연산자를 Lx, Ly, Lz라고 할 때, 그 3개의 각운동량의 곱을 더한 연산자 L^2를 Casimir operator라고 하며, 그것은 모든 각 운동량 연산자와 상호 호환관계에 있다. 따라서, Lz와 L^2은 동시에 대각화가 가능하고 같은 eigen space를 공유한다. 수식으로는 위의 말들을 아래와 같이 줄여서 얘기할 수 있다.

각 운동량 공간의 모든 상태는 진공 상태 (vacuum state)에 아래와 같은 ladder operator를 가함으로써 모두 쉽게 기술할 수 있다. 물리학자들이 때로는 슈뢰딩거 방정식 대신, 하이젠베르그의 행렬에 의한 방법을 선호하는 이유이다

SU(3)공간의 cartan subalgebra는 l3와 l8, 2개로 구성된다. 그 둘 외에 상호 호환 가능한 basis는 (앞서 살펴본 겔만 행렬) Gelmann 행렬 중에 없다. 그 둘을 각각 Isospin (I), Hypercharge (Y) 연산자라고 부른다. 그 둘은 동일한 eigen space를 공유한다. 이제 I와 Y에 관한 eigen value를 구해보면 각각 (1/2, -1/2), (1/3, 1/3, -2/3)이다. 이제, 아래 테이블을 보면, 왜 upquark의 spin 이 1/2, hypercharge가 1/3인지 이해가 갈 것이다. 우주에 관한 이해는 수에 대한 이해와 동일하다. 따라서 수학을 이해해야 우주에 대한 깊은 이해가 가능하다.

SU(3)공간에는 3개의 SU(2)공간이 존재한다. 따라서 3개의 ladder operator가 존재한다. 그 3개는 (u,d,s)를 1씩 증가시키는 역할을 한다. 아래에 가능한 ladder operator를 적어본다.

I+는 d=(0,1,0)을 u=(1,0,0)으로 변환시킨다. I-는 반대이다. U+는 s=(0,0,1)을 d=(0,1,0)으로 변환시킨다. U-는 반대이다.
위의 설명을 모두 이해했다면, Gelmann 8정도의 기본적인 그림인 아래 (u,d,s) quark를 벡터로 표시한 그림의 이해가 가능할 것이다. 이제, 8정도의 기본적인 이론을 이해한 것이다. 그 다음에는 Young tableau에 대한 이해가 필요하다. 이것은 meson이나 baryon같이 quark가 2개 혹은 3개가 gluon에 의해서 연결되어 존재하는 경우에 취할 수 있는 상태는 어떤 것이 있는가에 대해서 얘기한다.

'양자이론' 카테고리의 다른 글
| 반도체에 대한 단상 (0) | 2021.06.11 |
|---|---|
| 겔만, 리대수학과 팔정도 (2) | 2021.04.26 |
| 겔만, 팔정도 (0) | 2021.04.24 |
| 겔만, 입자 동물원을 정리한 팔정도 (0) | 2021.04.24 |
| 디락 방정식 I (0) | 2021.04.16 |




