겔만, 입자 동물원을 정리한 팔정도

어차피 한번은 할려고 했던 일이었다. 이번 회로 겔만 8정도를 모두 마무리하자. 8정도에 대해서 이제까지 3번정도의 게시를 하였다. 이번이 아마 마지막이 될 것이다. 입자 물리학의 입자 분류에 대해서 최종 정리하는 것이다. 그 다음은 강력, color space 상의 SU(3) 대칭성과, 글루온 라그랑지안의 독특한 성질로 인한 여러 강력의 성질들을 살펴보면 QCD에 대한 이해를 어느정도 정리한 것이 될 것이다. QCD 정리를 마치면, 양자역학->양자장->입자물리 혹은 고전역학, 전자기학, 양자역학, 상대성이론에 관한 많은 분야의 cover를 마치게 될 것같다. 언젠가는 해보고 싶었던 일이었고, 작년 10월부터, 부지런히 달려와서 종착역에 가까워지고 있다. 오늘 포스팅은 한꺼번에 마무리하고 싶어서, 비교적 긴 글이 될 것이다.

 

물리학자들은 무엇인가 단일한 기원이 있고, 단일한 설명이 있다면 좋겠다고 생각한다. 우주의 본질을 드러내는 하나의 공식, 하나의 입자에 대한 열망이다. 그 열망은 지금도 TOE(theory of everything)이라는 이름으로 진행되고 있다. 1950년대, 양성자와 중성자를 이루는 궁극적인 입자는 무엇인가.. 하고 대형 입자가속기로 그들을 파괴한다. 그 결과 나온 것은 온갖 정체 모를 파편들.. 규칙을 찾기에는 너무나 많은 종류의 입자들.. 대체 얘네들은 어디서 튀어나온 것인가? 우리가 뭔 짓을 한 것인가?

 

그러나, 그 입자들을 질량, 스핀,… blablabla하고 정리하다보니, 무엇인가 예사롭지 않은 규칙성이 있음을 천재 겔만은 직관한다. 평범한 사람의 눈에는 현상만이 보일 뿐이다. 그러나, 천재들의 눈에는 현상 저변의 본질, 수학적 구조들이 보이기 시작한다. 물론, 천재는 하늘에서 뚝 떨어지지는 않는다. 모든 진화는 현재까지 축적된 변화와 변이가 있기에 가능한 것이다. 하이젠베르그가 이미 Isospin이라는 개념을 제시하였고 이를 SU(2)라는 2차원 복소 공간의 회전 대칭성으로 파악하는 연구는 이루어졌다. 그리고, Yang-mills 이론에서 SU(3) 비가환 그룹에 대한 이론도 어느정도 전개되었었다. 겔만은 이들을 활용하여 그 복잡한 입자들을 (u,d,s) flavour 공간의 SU(3) 대칭성, 혹은 3차원 복소 공간에서의 회전 대칭성으로 정리한다. 이것이 겔만 8정도, Gellman Eight-fold way라고 부르는 입자 정리도이다.

 

아래 글은 그에 대한 글이다.

 

=========================================

 

우리 눈에 quark와 gluon은 직접 보이지 않는다. Quark는 color charge를 가지고 있고, 우리 눈에 color를 띤 입자들은 절대로 눈에 보이지 않기 때문이다. 오직, colorless 입자들만 눈에 관측될 뿐이다. 우리 눈에 보이는 입자들은 모두 composite particle들이다. 2개의 quark로 color를 없애는 방법은, quark/anti-quark의 조합밖에 없다. 그러한 입자를 우리는 meson이라고 부른다. 중간자이다. 가장 유명한 중간자는 pi meson 과 K meson이다.

 

만약 3개의 입자를 생각한다면 다양한 조합으로 color를 없앨 수 있다. 중성자 양성자 같은 바리온들은 3개의 quark로 구성된 composite particle들이다. 그들의 입자 분류표가 바로 Gellman 8정도이다. 처음에는 세상에는 up, down, strange의 3가지 종류의 quark만 있는 줄 알았다. 그 3개가 비교적 가볍고 쉽게 발견이 가능하기 때문이다. 그러나 그 후에 3개의 무거운 quark들이 고에너지 입자가속기 실험으로 계속 발견되었다. 그래서 현재까지는 (d,s,b), (u, c, t)의 6가지 종류의 quark가 존재함을 발견하였고, 그들 사이에는 다양한 변환룰들이 존재한다. (d,u)간에 Iso-spin 변환, (u,d,s)간의 flavour변환, (d,s,b)와 (u,c,t)간의 CKM 변환등 다양한 변환들을 여러 번의 포스팅으로 기술하였다.

 

quark자체가 기본입자이기에 기본 양자수 (I, B, S, Q 등)를 가진다. 그러한 입자들이 2개나 3개가 모이면 각 기본 입자들의 파동함수가 중첩되기 시작한다. 이 경우, 전체 파동함수는 대칭 혹은 반대칭의 여러 조합으로 나타날 수 있다. 그러한 조합이 몇가지가 있을까? 그것은 손으로도 계산할 수 있다. 예를 들어보자. (u,d)라는 두개의 입자가 있다고 가정하자. 그러면 (uu) (ud) (du) (dd) 등의 조합이 가능할 것이다. 그러나, ud와 du는 양자역학적으로는 (입자의 구분 불가능성으로 인해) 기본적으로 동일하다고 볼 수 있다. 그러나 (uu) (u+d) (u-d) (dd)로 하면, 기본적으로 대칭적인 입자 3가지(uu, u+d, dd)와 반대칭인 입자 1개(u-d), 총 4가지의 표현이 가능하다. 이것을 SU(2)를 표현하는 4개의 입자라고 부른다.

 

이런식으로 계산을 하면 N개의 상태를 가진(즉, 기본입자가 N개) M개의 기본 입자로 이루어진 모든 조합의 개수와 그 구성을 알 수 있다 (예를 들면 meson의 경우 N=3, M=2). 이것을 쉽게 graphical하게 계산 가능하게 하는 것이 바로 young tableau라고 불리는 방법이다. 여기에 대해서 알아보자.

 

Young tableau는 SU(N) group의 irreducible representation을 표현하는 방법에 관한 것이다. 그러한 입자가 1개 있다면 그 입자를 배치하는 방법은 1가지 밖에 없을 것이다. 그러나 그러한 입자가 N개가 가능하기에 아래 그림으로 표시할 수 있다. 입자 1개를 나열하는 방법이다. N가지 종류의 기본입자가 존재하기에 (예를 들면 SU(3)의 경우 (u,d,s)의 세종류) 그러한 입자는 N개 존재한다.

 

기본 입자가 M개 모인 경우에 몇 개의 composite particle이 가능할 것인가? 예를 들면 (u,d,s) 3종류를 가지는 2개의 입자의 모든 가능한 조합은 몇가지일 거인가? 이것과 유사한 문제가 입자 물리에서 가능한 meson입자의 종류는 몇가지인가일 것이다. 만약 3개의 입자를 가지고 만들 수 있는 조합의 수는 몇가지인가? 이 말은 baryon 입자는 몇 종류가 가능하고 그것들은 어떤 것인가에 대한 문제이다. 이 문제를 체계적으로, 직관적으로 푸는 방법은? Young tableau가 해결하려는 문제이다.

 

Young tableau의 모양을 살펴보자. 아래처럼 생겼다. 단순히 box가 쌓여있다. 제약 조건은 항상 그 위의 row의 개수는 아래 row의 개수보자 작지 않아야 하며, 왼쪽 column의 수가 오른쪽 column의 수보다 작지 않아야 한다. 가로와 세로의 의미는 무엇인가?

 

가로 방향은 해당 row에 존재하는 입자들이 대칭적으로 존재하는 것을 의미한다. 예를 들면, uu,  dd, ud+du의 경우 d와 u를 바꾸어도 대칭이다(부호가 그대로이다). U와 d만 가지고는 대칭적인 3가지 조합이 가능하다는 얘기이다. 세로 방향은 해당 column의 입자들의 반대칭적인 조합을 의미한다. 예를 들면 ud-du의 경우, u와 d의 위치를 교환하면 부호가 반전된다. 즉 column에 있는 어떤 2box를 교환하면 부호가 반대이다. 따라서 세로 방향으로는 같은 것들이 존재할 수가 없다. 예를 들어, 세로로 (uu)를 쌓으면 그 두개를 교환하여도 대칭이기에 규칙 위반이다. 따라서 세로 방향으로 최대 쌓을 수 있는 box는 N개를 넘을 수 없다 (모두 달라야 하므로). 이 말은 세로 방향으로 N개를 모두 나열하는 방법은 1가지 방법밖에 없고, 따라서, 세로로 N개의 box가 있다면 그것은 조합의 개수를 세는데에 무시해도 된다는 얘기이다. 아래 그림이 이를 설명한다.

 

이러한 일들을 왜 하는가? 그것은 애초의 문제, 즉 SU(N) 기본 particle M개로 이루어진 composite particle은 몇 종류이며 어떤 조합이 가능한가에 대한 대답을 얻기 위해서이다. 예를 들면 양성자 중성자는 모두 SU(3) particle 3개로 이루어진 composite particle이다. 그것 외에는 없는가? 있다면 몇 개 있고, 어떤 조합이 가능한가? 이것들을 모두 모아 놓으면 Gellman의 8정도에 나오는 바리온 8중항, 10중항 등에 해당할 것이다. 입자 물리에서는 각각의 입자들은 SU(N)의 irreducible representation에 해당한다고 얘기한다. 

 

정확히 어떻게 young tableau 방법을 생각했는지는 설명을 생략한다. 여기서는 단지 young tableau를 해석하는 방법만 소개한다.

 

1.young table의 모양이 주어진 경우, 몇 개의 가능한 조합이 있는가? 즉, young tableau의 dimension d는 얼마인가?

 

답은 d=num/den이다. num/den을 계산하는 방법은, 아래 그림에 주어진다. 위가 num을 구하는 공식이고 아래에는 den, 즉 hook number들의 곱을 구하는 문제이다. Hook number란 자신보다 아래 혹은 오른쪽에 있는 모든 박스의 수+1이다. 예를 들면 3은 자신의 오른쪽에 1개, 아래쪽에 1개 box가 있기에 그 자리에 3이라고 쓴 것이다. 이숫자들을 모두 곱하면 분모항 den을 구한 것이다. 왜 이런 공식이 나왔느냐는 가로는 교환에 대해 대칭인, 세로는 반대칭인 조합의 수를 계산하는 문제라는 것을 생각하고 서너시간 고민하면 이해할 수 있을 것이다. 

 

 

Gellman의 eightfold way에 8중항 10장항이라는 그림이 종종 나온다. 이것은 기본 입자들의 tensor product 혹은 direct product를 direct sum의 형태로 대체할 수 있다는 사실에서 나온다. 그 방법은 그냥 meson 혹은 baryon 의 경우를 예로 들어서 설명하면 가장 이해가 쉬울 것이다.

 

예를 들어 (u,d) iso spin 입자가 있다고 가정하자. 혹은 그냥 전자 1개가 up 혹은 down spin을 가지고 있다고 생각해도 좋다. 그러면 전자 2개가 모여서 quasi-particle을 이룬다고 가정하자. 그 입자가 취할 수 있는 모습은 몇가지인가? 양자역학에서 2개의 파동함수가 모이면 tensor product가 된다. 아래 그림의 제일 좌측을 나타낸다. SU(2)xSU(2)이다. 이제 오른쪽에 있는 1개의 box를 왼쪽에 있는 box에 쌓을 수 있는 방법은 가운데 있는 그림과 같은 2가지가 가능하다. 왼쪽은 symmtric한 3중항(triplet)와 단일항(singlet)의 합으로 나타낼 수 있다 (제일 오른쪽에 typo가 있는데 3+1임). SU(2) triplet는 spin 1인 입자이고, singlet는 spin 0인 입자이다. 즉, 스핀 1/2인 입자 둘이 모이면, 페르미온이 보존처럼 행동한다. 초전도 이론의 cooper pair가 이에 해당한다.

 

이제 위의 3중항 입자 2개를 모으면 어떤 입자가 가능한가? 아래 그림을 보면 알 수 있듯이 5중항 + 3중항 + singlet의 세 종류의 9개의 입자가 생긴다.

 

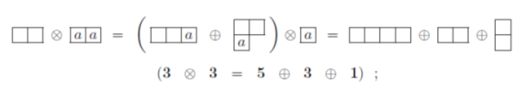
이 모든 과정은 SU(3)에 대해서도 그대로 적용이 가능하다. Meson의 경우 SU(3)상의 (quark, antiquark)의 조합으로 이루어진 quasi-particle이다. 가능한 meson 입자의 수는? 아래 그림에서 제일 좌측은 antiquark를 나타낸다. 그 오른쪽은 quark를 나타낸다. (u,d,s) quark가 가능하다고 생각하면 SU(3) 2개의 tensor 곱이다. 그 문제는 오른쪽 1개 box를 왼쪽 young tableau에 어떻게 붙이느냐의 문제이다. 오른쪽에 있듯이, 두가지 조합이 가능하다. Meson 8중항을 나타낸 것이다. 나머지 하나는 singlet이다.

 

이것이 바로 아래 그림을 나타낸 것이다. 8정도에 나오는 그림이다. Meson octet 라고 부르는 8개에 meson singlet (eta’)를 그린것이다.

 

바리온 입자에 대해서 알아보자. Baryon 은 SU(3) quark 3개로 구성되므로 아래 young diagram으로 나타낼 수 있다. 먼저 사각형 박스 2개로 만들 수 있는 방법은 아래의 첫번째 괄호와 같이 가로로 모두 연결하거나 세로로 모두 연결하는 두 방법이고, 여기에 1개의 box를 추가로 연결하는 방법은 아래 그림과 같이 4종류가 가능하다. 좌측부터 10중항, 8중항, singlet 항을 나타낸다.

 

즉, (u,d,s)로 표현되는 baryon 입자는 모두 4가지 종류로 구분이 가능하고 전체는 27종의 입자가 가능하다. 그 중 한 종류인 baryon 10중항의 그림은 아래와 같다.

 

1950년대 그 혼란스러워 보이던 수많은 입자들의 사태를 particle zoo라고 부른다. 아무런 규칙이 없어 보이던, 입자들에는 눈에 보이지 않은 수학적 구조가 내재해 있었다. 그것은 SU(N)이라고 부르는 group theory에 의해서 아름답게 묘사된다. Gellman은 10중항중 아직 발견되지 않았던 하나의 입자의 출현을 예상하고 양자수를 정확히 예측한다. 위의 그림에서 제일 아래에 있는 오메가 입자이다. 그리고, 그는 그 공로로 노벨상을 수상한다.