자신을 인식하는 물질, 존재와 의식... 자연철학적 접근
디락 방정식 I 본문
양자역학에서 여러 천재들이 등장한다. 그 중 세 손가락 안에 들 인물이 아마 Dirac일 것이다. 이번 포스팅에서 디락 방정식을 소개한다. 양자역학이 태동하면서 미시 세계에서 입자들은 파동 함수로 기술된다. 그 파동의 의미는 진폭의 제곱이 확률이다. 그 파는 다음과 같은 슈뢰딩거 방정식의 파동 방정식에 의해서 기술된다.

이것은 비 상대론적인 입자의 운동 방정식이다. 그 다음 단계는 당연히 빛 입자의 움직임을 양자적으로 묘사하는 것이다. 즉, 상대성이론과 양자역학의 결합을 시도한다. 그런데, 위의 방정식은 조금 문제가 있다. 왜냐하면 상대성 이론에 따르면 시간과 공간은 동일한 취급을 받는 하나의 좌표계에 지나지 않는데, 위의 방정식은 시간에 대해서는 1차 미분, 공간에 대해서는 2차 미분의 형태이므로 시간을 공간과 분리된 어떤 특별한 존재인 것처럼 취급하기 때문이다. 시공간에서 (ct, x, y, z) 는 모두 길이의 단위이고 시간은 방향성만 제외한다면 특별한 변수가 아니다. 그러나 슈뢰딩거 방정식은 그렇지 않다.
1.Derivation of Klein-Gordon(K-G) equation
상대성 이론에 따르면 에너지는 다음과 같은 수식으로 묘사된다. 특수 상대성이론의 결과이다.

양자역학과 고전역학의 가장 큰 차이는 우리가 관측하는 어떤 물리량에 해당하는 연산자가 존재하는 것이며, 연산자와 파동함수의 관계에 의해서 물리량이 관측된다는 것이다. 다른 말로는 observable은 Hermitian operator이고, operator의 expectation을 우리는 관측하는 것이다. 이제 위의 p와 E에 각각에 해당하는 연산자를 대입하면
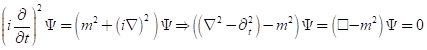
와 같은 klein-gordon 방정식이 유도된다. 상대론적인 슈뢰딩거방정식이다. 위에서 사각형박스는 D'Alembert (라플라스이 스승) 방정식이라고 부르고 만약 시간에 대한 미분이 없다면 Laplacian 연산자이다. 위 방정식와 아래 모든 방정식의 전개에서 흔히 물리학 책에서 가정하듯이 h-bar=c=1로 둔다.
조금 더 formal하게 유도하자면 양자장론으로 다음과 같이 유도할 수 있다. Phi(x) 혹은 phi(x,y,z)를 양자장, quantum field라고 하자. 양자장은, 3차원 공간의 한점마다 한 개의 자유도를 가지는 입자의 장이라고 생각하면 된다. 양자장이 vacuum state에 있으면 입자가 없고, 아니면 입자는 관측된다. 양자장이 Lorentz변환에 대해서, 즉 4차원 시공간의 회전 변환에 대해서 불변이 되기 위해서는 Lagrangian이 아래와 같이 제곱항으로 주어져야 한다. 이것이 유일하지는 않지만, 보통 양자장론에서 말하는 free particle의 움직임을 기술하는 라그랑지안이다.

여기에 대해서 Euler-Lagrange 방정식을 적용하면

2. Problems of K-G equation – negative probability
위의 방정식은 시간에 대해서도 공간에 대해서도 모두 2차 함수이므로, 시간과 공간 좌표계가 동일한 취급을 받으므로 상대성 이론의 기본 원리에 충실하다. 위의 방정식은 파동 방정식이고 그 해는 아래와 같다.

문제도 유도했고, 상대성 원리에도 맞고 … 다 좋은 것 같은데 klein-gordon 방정식은 치명적인 문제점을 안고 있다. 먼저, K-G 방정식으로부터 probability density 와 probability current를 다음과 같이 유도해 보자. 연속 방정식과 완벽하게 동일한 형식이다.

이제 K-G 방정식의 해로부터, probability density를 구해 보자.

K-G 방정식, 그리고 이어서 나올 Dirac 방정식 모두, 음의 에너지의 해를 가진다. 즉, 제일 위의 방정식으로부터 E=+ 혹은 – sqrt(m^2+p^2) 이므로 양과 음의 에너지의 E값, 즉 양의 해와 음의 해를 가진다. 에너지는 어차피 상대적인 양이므로 음의 에너지는 이해가 된다. 그러나, 위에서 보듯이 음의 에너지는 음의 확률을 의미하는데, 음의 확률이란 수학적으로 허용하기 어려운 개념이기에 위의 K-G는 한동안 잊혀진다.
3.Dirac equation
이제, 양자역학의 여러 거대 영웅 중 한명인 Dirac의 기발한 접근법을 알아 보자. Dirac 은 먼저 KG 방정식을 인수분해한다. 이 까지는 아무나 생각할 수 있다. 그러나, 기본적으로 K-G 방정식은 숫자만으로는 인수 분해가 불가능하다. 시도해 보면 안다. 디락은, “왜 꼭 숫자여야 하나? 숫자 자체도 하나의 추상적 기호에 따름 아니냐?” 라는 발상의 전환을 한다.

위 방정식에서 b와 g은 왜 필요한가? 왜냐하면 그것이 없으면 절대 위의 관계를 만족시킬 수 없기 때문이다 (즉 인수분해가 안되기 때문이다). 그리고, 그 값이 scalar 값, 즉 어떤 실수값인 경우도 절대로 위의 형태로 인수분해가 안되고, 그것이 인수분해가 되려면 그 두 값은 행렬 형태로 주어져야 하며 특정한 수학적 구조를 만족해야 한다. 이렇나 수학적 구조, 즉, {.,.}연산을 가진 대수 구조체를 Clifford algebra라고 부른다.
이제 KG방정식은 인수분해된 한 쪽 pair인 다음 방정식을 만족해야 한다. 다음 방정식이 그 유명한 Dirac 방정식이며, 양자역학/양자장론/게이지 이론을 이해하려면 반드시 만나게 되는 방정식이다. 기호가 마치 삭제 표시와 비슷한 요상하게 생긴 방정식이다. K-G 방정식이 2차 미분 방정식인데 비해, Dirac 방정식은 1차 미분 방정식인데, 행렬 방정식이다.

이제 나머지 행렬들이 모두 4x4 형태이므로 Y는 4x1 의 벡터와 비슷한 형태의 수학적 구조이며 이를 스피너 혹은 bi-spinor라고 부른다.
다음 포스팅에서는 디락방정식의 해를 살펴보자. 이 과정에서 전자의 다른 짝인 양전자가 소개된다.
==========================
수학에 좀 더 관심이 있다면
4. Properties of Gamma matrices
디락 행렬 혹은 gamma matrix는 4x4 행렬이고 그것들은 Clifford algebra를 만족시키는 행렬들이다. Clifford algebra에 대해서는 나중에 상세히 설명하기로 하고, 그 대수적인 구조를 먼저 간단히 기술해 보자. 아래 수식에서 보듯이 gamma matrix는 Pauli 행렬로부터 정의된다.

당장의 디락 방정식에는 소용이 없지만, parity 대칭성을 설명하려면, chirality를 설명해야 하고, 이를 위해서 다음과 같은 추가의 행렬을 정의한다.

'양자이론' 카테고리의 다른 글
| 겔만, 팔정도 (0) | 2021.04.24 |
|---|---|
| 겔만, 입자 동물원을 정리한 팔정도 (0) | 2021.04.24 |
| 디락 방정식 II (0) | 2021.04.16 |
| 자연은 왼손잡이 (0) | 2021.04.15 |
| Ising model, 이징 모델 (0) | 2021.03.08 |




