자신을 인식하는 물질, 존재와 의식... 자연철학적 접근
로렌츠 변환의 의미 본문
두 개의 관성 좌표계가 있다고 하자. 하나는 (x,t) 이고 다른 하나는 (x’,t’)이다. 아래 그림에서 (x,y)는 예를 들면 정지한 좌표계이고, (x’,y’)는 x축으로 v라는 속력으로 이동하는 좌표계이다. 정지한 사람이 바라본 (x’,y’)=(0,0) 점은 (ut, 0) 이고 반대로 이동하는 사람을 중심으로 보면 원점은 (-ut, 0)이다. 누구를 기준으로 생각하느냐에 따라 움직임은 대칭적이고 상대적이다.
두 좌표계에서 모두 동일한 광속을 측정해야 한다. 광속 불변을 설명하기 위한 변환 관계가 로렌츠 변환이다. 유도해 보자. 선형 변환으로 설명이 가능하면 제일 간단하므로, 아래와 같이 두 좌표 사이에 선형 변환의 관계에 있다고 가정해 보자.

앞서 배운 행렬식을 이용하여 시간과 x축만을 고려한 선형 변환 관계를 설명하면 아래 수식과 같다. 광속 불변을 설명할 수 있게, 상대성 원리가 성립할 수 있게 A, B, C, D를 구해 보자.

위쪽에 있는 식은, 정지한 사람이 바라본 이동 좌표계의 원점 x’=0로부터 관계식을 유도한 것이고, 아래에 있는 수식은 이동 좌표계에서 정지 좌표계의 원점을 바라본 경우이다. 그 관계식의 결론은 A=D, C=-Av라는 사실이다. 이것을 이용하면, 위의 방정식은 아래와 같이 간단히 나타낼 수 있다.

만약, (t’, x’)를 원래 좌표계로 생각하고 (t,x)를 이동하는 좌표계로 생각했다면 동일한 결과를 얻었어야 하므로, 즉, 운동의 상호 대칭성을 고려하면 A값을 구할 수 있다. A를 gamma(g)로 표시하고 이것을 Lorentz factor라고 부른다.

이제 K값만 결정하면 로렌츠 변환을 모두 유도한 것이다.
두 좌표계에서 광속이 불변이어야 하므로
ct’=x’ -> c(t+Kx)=-vt+x, 양변을 t로 나누면 c(1+Kc)=-v+c 따라서 K=-v/c^2
완성된 공식은

위의 변환을 로렌츠 변환(Lorentz transform)이라고 부른다. 만약 t,x와 t’,x’의 위치를 바꾸면 -부호가 사라진다.
로렌츠 변환을 조금 수학적으로 어렵게 이해하면 아래와 같이 나타낼 수 있다.

위에서 cosh(x)와 sinh(x)는 hypobolic function이라고 불리며 아래와 같이 정의되며 cos2+sin2=1인데 반해서 그 함수들은 cosh2-sinh2=1인 관계를 만족시키며, 그 단순한 하나의 사실이 우주 공간을 유클리드 공간에서 4차원 민코프스키 공간으로 변환시킨다.

아래와 같은 좌표 변환을 생각해 보자. 두개의 지점 (x1,y1), (x2,y2)사이의 거리를 delta (X)=(dx,dy)=(x2-x1, y2-y1)이라고 하자. 즉, 유클리드 공간의 두 점 사이의 거리는 아래와 같이 주어진다.

이제 x,y 축이 각도 a 만큼 회전된 좌표계를 생각하면, 그렇게 회전된 좌표와 원래 좌표상의 관계식은 아래와 같은 행렬식으로 주어진다. 회전 변환을 나타내는 행렬을 R이라고 하면 R^TR=I이다. 이러한 성질을 만족하는 행렬을 orthogonal matrix라고 한다. 직교행렬이다. 직교 행렬은 회전, 혹은 축대칭 변환을 나타낸다.
회전 변환은 아래에서 보듯이, 유클리드 공간에서 두 지점 사이의 거리 delta X를 보존한다.

Minkowski 공간은 이전 포스팅에서 보았듯이, 4차원 시공간의 두 지점 사이의 거리가 아래와 같이 정의된다.

이제 로렌츠 변환 행렬을 다르게 변환해보자. 즉, 4차원 공간의 두 이벤트 사이의 거리, space time interval을 보존해야 한다는 조건으로부터

즉, 로렌츠 변환이란 L^TgL=g를 만족하는 행렬로 나타내어지는 변환이다. 이 조건을 만족하면 좌표 변환을 했을 때, space time interval을, 그리고 모든 로렌츠 변환 좌표계 간의 광속 불변을 보존한다. 이것을 Minkowski 공간의 회전 변환으로 이해하면 편리하다.
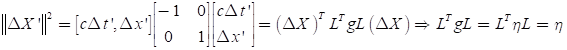
Space time interval 은 S=(cdt)^2-(dx^2) 로 정의고, 양수 2개의 빼기로 정의되므로 ><=0의 세가지 case가 발생할 수 있다.
만약 S>0이면 time-like, S<0 이면 space-like, S=0이면 null event가 발생한 것으로 부른다. 운동하는 사람이 가지고 있는 시계로 측정한 시간을 고유시간 (proper time)이라고 부른다.

만약 기차가 0.8c로 움직이고, 그 기차에서 총을 쏘고 총알이 0.6c로 움직인다면, 외부에서 보았을 때, 총알은 얼마의 속도로 날아갈까? 단순히 생각하면 0.8c에서 0.6c로 쏘는 것이니 1.4c가 되어, 광속을 넘어서겠죠? 그것은 불가능합니다.
정지 좌표계를 (t, x) 이동 좌표계를 (t’,x’)라고 하자. 정지한 사람이 바라본 속력이므로 우리는 dx/dt를 구해야 한다. 앞 장의 게시글로부터, 두 좌표계 간의 로렌츠 변환식은 아래와 같다. 이제 로렌츠 변환식을 이용하여 그 문제를 풀어보면

와 같이 되어, 광속의 0.95배로 날아가는 것처럼 보인다. 위의 오른쪽 관계식을 보면 알 수 있듯이, u와 v가 c가 되어도 최대 속력은 c가 되어, 광속을 결코 넘어설 수 없다.
고전적인 갈릴레오의 상대성 원리는 그냥 두 속도를 합하면 되지만, 상대성이론에서의 상대속도는 위의 공식과 같이 구해야 한다.
혹은 hyperbolic rotation 공식을 이용하면
즉, hyperbolic space에서의 각도가 속도임을 안다면 위와 같이, 두 속도의 합을 tanh 공식으로부터 쉽게 유도할 수 있다.

'상대성이론' 카테고리의 다른 글
| 전자기학의 텐서 표현 (0) | 2021.01.29 |
|---|---|
| 레비시비타 심볼 (0) | 2021.01.29 |
| Four momentum (0) | 2021.01.27 |
| 일반상대성이론 기본 공리 (0) | 2021.01.27 |
| 상대성이론과 전자기학 (0) | 2021.01.26 |




