자신을 인식하는 물질, 존재와 의식... 자연철학적 접근
휘어진 공간에서의 관성의 법칙 본문
일반 상대성이론에서는 휘어진 4차원 시공간을 얘기한다. 휘어진 시공간에 대해서 무엇을 얘기할 수 있을 것인가?
휘어진 시공간에서 관성의 법칙이 무엇인지를 얘기할 수 있을 것이다. 즉, 평면에서의 관성의 법칙은 직선 운동을 의미한다. 물리학은 무엇을 얘기하는가? 대칭과 대칭에 따른 보존량을 얘기한다. 이 말의 의미를 정확히 이해한다면 물리학에 대해서 어느 정도는 관심이 있는 분일 것이다. 왜 평면에서 외력이 없으면 직선 운동을 하는가? 우리의 시공간이 병진 대칭성 (translation symmetry)가 있기 때문이고 그에 따라 운동량이 보존되기 때문이다.
휘어진 공간에서 존재들은 외력이 없다면 곡선운동을 한다. 휘어진 구간의 두 지점 A와 B사이의 가장 길이가 짧은 경로를 따라 존재들은 움직이고 에너지와 운동량이 보존된다. 그러한 경로를 geodesic, 측지선이라고 부른다. 아인슈타인의 일반상대성이론의 첫번째 큰 주제는 metric이 주어진 일반적인 곡면에서의 측지선은 무엇인가에 대한 수식을 유도하는 것이었다.
휘어진 공간에서 측지선을 따라 움직이는 것을 우리는 외부에서 중력이 작용하여 물체가 떨어졌다고 부른다. 즉 3+1차원의 중력이론은 4차원 시공간에서는 관성의 법칙에 지나지 않는다.
두번째로는 무엇을 얘기할 수 있는가? 도대체 시공간은 왜 휘어졌을까하는 것이다. 시공간을 휘어지게 만든 것은 에너지이다.
여기까지의 얘기는 문돌이던 공돌이던, 물리학에 관심이 있던, 그냥 물리학을 아는척하고 싶어하는 이들이든 쉽게 얘기할 수 있다. 그러나 좀 더 관심이 있다면, 좀 더 사냥에 대한 야생성을 가지고 있다면, 우리가 측지선이라고 부르는 것이 무엇인지, 측지선을 따라 이동하는 것이 과연 뉴턴역학으로 구한 중력과 동일한지, 에너지는 얼마나 시공간을 휘어지게 하는지 쫓아가고 싶을 것이다.
======================================
이전 포스팅에서 리만 텐서를 소개하였다. 공간이 휘어진 경우에 한 벡터를 폐 경로 (close path)를 따라 평행이동 (parallel transport) 하면 원래 벡터로 돌아오지 않는다. 즉,

즉, 서로 다른 두 경로로 한 벡터를 parallel transport 했을 때, 원래 벡터와 어떠한 차이가 있는지를 리만텐서가 알려준다. 리만 텐서는 인덱스가 4개 달린 4차의 rank 4 tensor임을 설명하였다. 이것을 축약하면 리치 텐서와 리치 스칼라를 얻는다. Metric tensor의 2차 미분 공간이 원래 벡터와 선형 적인 관계에 있다는 것도 재미있는 사실이다.
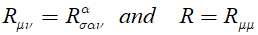
리만 텐서가 0인 공간에서 당연히 리치 텐서도 리치 스칼라도 0이다. 이를 flat minkowski space라고 부른다. 즉, 공간이 평탄하다는 얘기이다.
그러면 반대로 리치 텐서가 0이면 리만텐서는 0일까? 당연히 아니다. 그러면 리치 텐서가 0의 의미는 무엇인가? 그것은 그 공간에 물질이 존재하지 않는다는 것이다. 즉, 블랙홀의 외부, 태양의 외부, 지구의 외부 공간을 말한다. 그 공간에 물질은 존재하지 않지만, 공간은 주변에 존재하는 물질의 영향으로 휘어져있다.
아인슈타인인의 장 방정식은 자연스럽게 도출된 것은 아니다. 이 부분에서 아인슈타인의 직관이 눈에 띈다. 아인슈타인의 논리를 쫓아가 보자. 먼저 예전에 포스팅한 휘어진 공간의 직선의 방정식, geodesic equation으로부터 얘기를 시작해 보자.

만약 중력이 없다면, 질량원에서 아주 먼 곳이라면 공간은 평탄하고 g_mn=eta_mn으로 flat Minknoski 공간이다. 이 공간에서 metric의 미분은 0이고, Christoffel = 0 이고, 그냥 관성의 법칙에 따라 일정속도로 운동을 진행한다.
이제 질량원의 질량이 작거나, 질량원에서 어느 정도 거리가 떨어져서 공간의 휘어짐이 작다고 혹은 중력이 작다고 가정하고 geodesic equation을 풀어보자. 그리고, 질량원이 시간에 따른 변화가 없다고 가정한다. 위의 가정에 따라 아래 관계식이 성립한다.

첫번째 식은 metric의 시간에 따른 변화가 없다라는 가정에 따른 것이고, 두번째,세번째 수식은 중력이 약하고 이동하는 물체의 속력이 느리다는 가정에서 나온 것이다. 위 조건을 geodesic 방정식에 적용하면 계산해야 할 항은 다음과 같이 3개의 공간에 대한 항 밖에 없다.

중력이 약한 공간, metric이 살짝 휘어진 공간에서 뉴턴 법칙이 유효하므로, metric이 다음과 같이 표시된다고 가정하면 아래와 같이 metric은 (-1,1,1,1)로 표시되는 flat space metric과 아주 작은 변이항의 합으로 표시할 수 있다.

이제 geodesic 방정식을 푸는데 필요한Christoffel symbol은 다음과 같이 근사적으로 표현된다. 간단한 관계식이다.

고전적인 뉴턴의 중력 방정식은 아래와 같이 중력 potential 식으로 표현된다. 아래에서 중력가속도와 관성가속도는 동일하다는 가정이 적용되었고, 중력은 중력장 혹은 중력 포텐셜 필드의 미분으로 표시된다는 간단한 내용을 수식으로 나타낸 것이다.

위의 방정식과 앞서 구한 geodesic 근사 방정식을 비교해 보면

위의 전체 과정을 Weak field approximation of gravity 라고 부른다. 일반 상대성이론책에 모두 소개되는 내용이다.
이 수식의 의미는 중력 potential 에 해당하는 항이 바로 metric 에 의해서 결정된다는 것이다. 즉, metric의 휘어짐이 힘으로 느껴진다는 일반상대성 이론의 원리로 연결된다. 아래 식에서 r=2GM이 그 유명한 schwartz radius, 블랙홀의 크기를 나타낸다. 반경이 2GM이 되면 g00=0이 되어, 외부에서 바라본 블랙홀의 시간은 정지한다. 사건의 지평선이다.
태양의 주변에서 조차도 평탄한 곳에 비해서 10^(-6) 정도 휘어졌을 뿐이데, 우리는 이 작은 공간의 휘어짐을 어마어마한 중력으로 느낀다. 나머지 이야기는 다음 포스팅으로 미룬다.
'상대성이론' 카테고리의 다른 글
| 수성 근일점 문제 - 케플러 법칙 증명 (0) | 2021.02.25 |
|---|---|
| 아인슈타인의 Field equation, 장 방정식 (0) | 2021.02.05 |
| 일반상대성이론-아인슈타인 장 방정식 (0) | 2021.02.03 |
| Parallel transport (0) | 2021.02.02 |
| 전자기학의 텐서 표현 (0) | 2021.01.29 |




