자신을 인식하는 물질, 존재와 의식... 자연철학적 접근
통계역학 - 보존과 페르미온 통계 본문
우리가 흔히 입자라고 부르는 것들은 크게는 boson 입자와 ferimion 입자로 두 종류로 나눠진다. 우리 밴드에 있는 이들 중 보존과 페르미온을 모르는 이는 없을 것이다. 입자들은 파동처럼 존재하고, 입자가 bounded potential 에 존재하면, 어떤 경계조건이 존재하면 그것을 맞추는 입자들만 동위상으로 배열되어 살아남기에 quantized 양자 수를 가지게 된다.

고등학교 화학 시간에 n, l, m, s라고 부르는 4개의 양자수가 있고 각각은 주양자수, 부양자수, 자기 양자수, 스핀 양자수라고 부른다. 주양자수는 에너지를 결정하고, (n,l)은 각운동량을, 그리고 점입자이기에 절대로 고전적으로 묘사가 어려운, 스핀이 그것들이다. 스핀은 제자리에서 자전을 하는 것이다. 왜 전자를 자전한다고 그냥 얘기하면 안되는가? 전자가 점입자인데 자전으로 스핀을 설명하려면 자전 속도가 광속을 넘어야 하기에 고전적으로 묘사는 불가능하다.

인간들이 우주의 모든 것을 다 아는 것처럼 얘기하지만, 빛 알갱이 하나, 전자 하나의 본질도 전혀 모르고 있다. 고전 통계역학은 볼츠만 분포만 존재하지만 양자 통계역학에서는 입자의 성질에 따라 볼츠만, 페르미디락, 보즈아인슈타인의 3가지 종류의 통계를 가진다. 아래는 이에 대한 수학적인 내용이다.

================================================
통계역학에서는 3가지 분포에 대해서 얘기한다. Maxwell-boltzmann, Fermi-dirac, Bose-Einstein statistics(distribution)이 그것들이다. 뒤의 두개는 quantum mechanics를 반영하였고 전자의 경우는 고전적인 입자에 관한 통계이다. 전자인, Maxwell-Boltzmann 분포는 이미 다루었다. 나머지 두 개의 분포에 대해서 이번에 다뤄보자. 이번 session에는 통계역학의 정리를 목표로 내용을 정리하고 있다. 물론, 내용은 모두 외국 대학 강의 노트에 있는 평범한 내용들이다.
N개의입자로 이루어진 시스템을 생각하자. 시스템이 상태 R에 있을 때, 각 입자들이 에너지 레벨 r=1,2,…에 n_r개씩 분포한다고 가정하자. 시스템 전체의 에너지는 E_R이라고 하자.

Canonical ensemble의 경우, 온도와 V는 일정한데 비해 에너지의 이동은 자유롭기에 시스템의 에너지는 변할 수 있으며, 이 경우 통계역학에서 가장 중요한 물리량인 partition function Z는 아래와 같이 주어진다.

이제 에너지 상태 Es에 존재하는 particle 수의 평균을 구해 보면 아래와 같다.

세가지 통계가 존재한다. 각각은 Maxwell-Boltzmann, Fermi-dirac, Bose-einstein statistics이다. 각각의 이해는 통계역학의 이해에 필수적이며, 만약 반도체의 동작원리나 고체 물리에 관심이 있다면 더더욱 정확히 이해해야 한다.
1.Maxwell-Boltzmann statistics
MB 분포는 고전적인 입자를 가정한다. 고전 역학에서 각각의 입자는 구별이 가능하다. 그러나 동일 입자라면 동일한 확률 분포를 가질 것이다. 이 경우에 partition function은

이것은 다른 방법으로도 유도가 가능하다. 즉 system의 모든 가능한 상태 R에 대해서 Boltzmann factor를 모두 더하면 partition function Z를 구할 수 있다. 단, 시스템내의 입자의 이동은 자유롭지 않고 N으로 제한된다. 이 경우 Z는 아래와 같이 주어진다.

이제 시스템의 configuration을 입자의 수 측면에서 나열해 보자. 즉 n1, n2,… 개의 입자 분포를 가지는 경우에 대해서 모두 생각해 보자. 고전역학적으로는 모든 입자들은 구분이 가능하기에 n1,n2,… 개의 분포가 주어지면 가능한 상태의 수는 N!/(n1!n2!...)이 된다 (고등학교에 나오는 얘기이다). 이제 입자의 수 측면에서 partition function을 구해 보면, 앞서의 결과와 동일한 결과를 얻는다.

2.Bose-einstein statistics
Photon의 경우의 입자수 보존의 법칙은 의미가 없다. 전자의 에너지 상태가 변하는 경우, photon은 무에서 유로 탄생한다. 에너지 레벨 차이에 따라 쎈 photon 1넘 혹은 약한 photon 2넘이 나올 수도 있다. 그리고, 다른 전자를 만나서 photon은 사라질 수도 있다. 그리고, boson은 하나의 양자 상태를 이론적으로 무한개의 입자들이 점유할 수 있다. 이러한 입자의 통계는 BE(bose Einstein) 통계를 따른다.

같은 boson 입자라도 phonon의 경우는 photon과 다르게 입자수 보존의 법칙이 성립해야 한다. 이 경우의 통계는 아래와 같다.
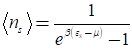
3. Fermi-dirac statistics
Fermion의 spin 은 1/2의 배수이다. 이 경우, 두 개의 입자를 서로 교환하면 파동함수는 원래와 반대 위상이 된다. 만약 두개의 입자가 동일입자이고 파동함수가 동일하다면 파동함수는 사라진다. 이것을 Pauli의 exclusion principle (파울리 배타 원리)라고 부른다. 두개의 동일한 입자는 같은 양자 상태를 점유할 수 없다. 따라서
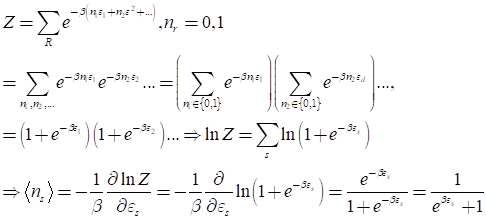
만약 입자의 수가 N으로 제한되어 있다면

로 주어지며, 위에서 mu를 chemical potential 이라고 부른다. 반도체의 원리를 이해하려면, Fermi-dirac 통계의 의미를 정확히 이해하고 있어야 한다. 이것은 에너지 대역 epsilon에 양자 상태가 존재할 때, 그 양자 상태를 전자가 점유할 확률을 나타낸다.
만약, 별의 내부에서 어떤 일이 이루어지고 있는지를 정확히 이해하려면 위에서 얘기한 내용들을 알고 있으면 이해에 도움이 될 것이다.
'양자이론' 카테고리의 다른 글
| 전자 축퇴압 (0) | 2021.02.23 |
|---|---|
| 통계역학, 브라운 운동과 확산 (0) | 2021.02.19 |
| 와인과 아레니우스 방정식 (0) | 2021.02.17 |
| 열역학-자유에너지 (0) | 2021.02.16 |
| 열역학 법칙들 (0) | 2021.02.15 |




